Seja :
Calcule , , e ;
Verifique que e determine os intervalos de crescimento e decrescimento de ;
Estude a concavidade de ;
Pesquise a existência de assíntotas em e ; esboce o gráfico de .
Passo 1
Vamos calcular os limites pedidos, levando em conta que o domínio da função corresponde a :
Passo 2
Precisamos agora derivar a função, sendo o resultado esperado esse:
Vamos derivar pela Regra do Quociente.
Ora, achamos o resultado esperado.
Passo 3
Pensando agora no crescimento da função , temos que levar em conta a análise de seu sinal. Sabendo que a derivada é composta por três termos e um deles, o , é sempre positivo, o sinal só depende dos dois outros termos. Vamos analisar o quadro de sinais para descobrir aonde a derivada de é positiva ( crescente) e onde é negativa ( decrescente):
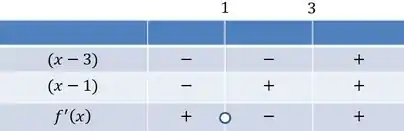
Como vemos, a função será crescente em e decrescente em , sendo um ponto crítico de mínimo local, já que a derivada é negativa antes dele e positiva depois, sendo nula em .
Passo 4
Para o estudo da concavidade derivamos pela segunda vez a função e analisamos seu sinal. Usamos, novamente, a Regra do Quociente:
Ora, como é uma potência par e será, portanto, sempre positiva, vemos que o sinal da derivada segunda depende apenas de , que é positivo para e negativo para .
Ou seja, a função é côncava para cima em , para baixo em e tem ponto de inflexão em .
Passo 5
Procuramos agora as assíntotas. Já sabemos que, pela descontinuidade em , temos uma assíntota vertical nesse ponto. Agora, como os limites quando e explodem, respectivamente, para e , notamos que não existem assíntotas horizontais. Nesse caso, vamos procurar a existência de assíntotas oblíquas na forma de uma reta modelada por . Por definição, calculamos e para o lado do :
Fazemos a mesma coisa para , modelando a assíntota oblíqua por :
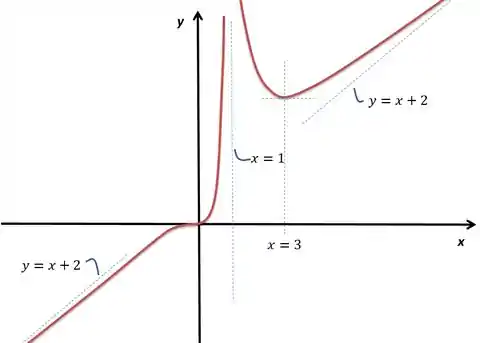
Enfim, concluímos que tanto para quanto para a assíntota oblíqua para a qual o gráfico se aproxima é !
Passo 6
Vamos reunir as informações da questão:
- Domínio de : .
- Limites importantes
- Função é crescente em e decrescente em , sendo um ponto crítico de mínimo local.
- A função é côncava para cima em , para baixo em e tem ponto de inflexão em .
- Ass. verticais: ; Ass. Horizontal: ; Ass. Oblíqua: (para )
Vamos esboçar o gráfico com o que temos, dado que e :