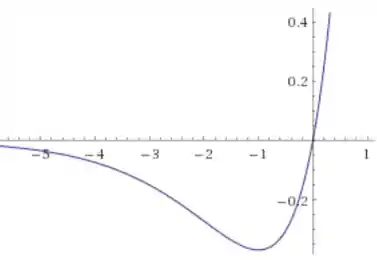
5. Esboce o gráfico da função , destacando todos os passos utilizados.
Passo 1
Oi, galerinha! Tudo bom? Essa é uma questão que pede para esboçarmos os gráficos e destacar cada passo realizado.
Vamos começar entendendo o domínio da função! Repara que temos a seguinte função
Nossa, função é um produto de uma função polinomial e uma função exponencial . Ambas funções são continuas e existem para qualquer ponto. Logo nosso domínio será todos os reais.
Bora o próximo passo!
Passo 2
Agora vamos achar os pontos críticos! Para isso precisamos derivar a nossa função e igualar a zero.
Aplicando a regra da cadeia para derivar ficamos com
Igualando a zero, ficamos com
Logo, é o único ponto crítico da função. Agora vamos analisar o seu entorno!
Para , temos que (aqui se você quiser conferir, pode escolher qualquer valor valor menor que e substituir na derivada para encontrar um valor negativo). E para , temos (se quiser conferir aqui também, sem problemas). Logo é descrecente em valor menores que e crescente em valores maior que , o que mostra que é uma mínimo local.
Passo 3
Agora que já sabemos que é um mínimo local, vamos descobrir quanto ele vale, jogando esse valor na função:
Note que .
Passo 4
Agora vamos analisar a segunda derivada e descobrir se temos um ponto de inflexão!
Fazendo a segunda derivada temos,
Igualando a zero ficamos com
Agora vamos analisar o seu entorno, seguindo o mesmo raciocinio da primeira derivada!
Para , temos que e para , temos . Logo é côncava para baixo em valores menores que e côncava para cima em valores maiores que , o que mostra que é um ponto de inflexão.
Passo 5
Outra possibilidade que temos que considerar é a existência de assíntotas verticais. Os pontos candidatos a assíntotas verticais são aqueles em que a função não existe, então verificamos se o limite tendendo àquele ponto vai para infinito.
Neste caso, temos que e é contínua em , como vimos no Passo 1. Logo não há assíntotas verticais.
Passo 6
Agora vamos para as assíntotas horizontais! Para encontrá-las precisamos verificar os limites tendendo a infinito. Fica assim
Ou seja, não há assíntota horizontal em .
Agora vamos analisar para . Fica assim,
Temos uma indeterminação. Então, vamos reescrever essa função e aplicar L’Hospital.
Derivando em cima e embaixo,
Logo, em temos uma assíntota horizontal em .
Passo 7
Agora vamos procurar assíntotas oblíquas. Como já encontramos uma assíntota horizontal para , faremos apenas para .
Para encontrar assíntotas oblíquas, calculamos
Logo, não há assíntotas oblíquas.
Passo 8
Agora vamos encontrar o ponto em que a função cruza o eixo y, calculando
Ou seja, a função corta o ponto . Então já achamos ao mesmo tempo a raíz da função.
Passo 9
Por fim, vamos juntar todas as informações encontradas nos passos anteriores e montar o gráfico. Fica assim:
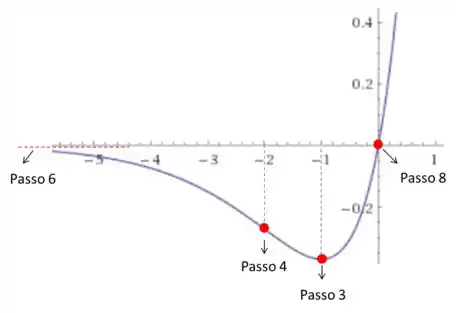
Resposta