Seja
- Determine os intervalos de crescimento/decrescimento de , e os seus pontos de máximo/minimo
- Determine os intervalos onde é côncava para cima/baixo e os seus pontos de inflexão
- Caso existam, encontre as assíntotas horizontais e verticais
- Esboce o gráfico de usando (pelo menos) as informações obtidas nos itens , e
Passo 1
Para saber os intervalos de crescimento e decrescimento temos que analisar o sinal da derivada de .
Sabendo que é uma parábola de concavidade para cima, podemos afirmar que:
Passo 2
Como a função muda de crescente para decrescente em , esse é um ponto de máximo da função. E como a função muda de decrescente para crescente em , esse é um ponto de mínimo.
Passo 3
Temos que descobrir onde a função é côncava pra cima ou côncava pra baixo. Como fazer isso? Analisando o sinal da segunda derivada
O termo sempre é positivo, logo o sinal de só depende da parábola . Vamos achar suas raízes.
Como essa parábola tem concavidade para cima, sabemos que:
Passo 4
Os pontos de inflexão são os pontos onde a função muda de concavidade. Nesse caso, são os pontos
e
Passo 5
Pra calcular as assíntotas horizontais temos que fazer os limites com . Vamos lá:
Podemos aplicar L’Hopital nesse limite se escrevermos dessa forma:
Aplicando:
Aplicando L’Hopital de novo:
Há uma assíntota horizontal em .
Passo 6
As assíntotas verticais só existem se a função tiver descontinuidade. Nesse caso, a função é contínua para todo . Por isso, não há assíntotas verticais.
Passo 7
Juntando tudo que descobrimos nos passos anteriores podemos esboçar o gráfico:
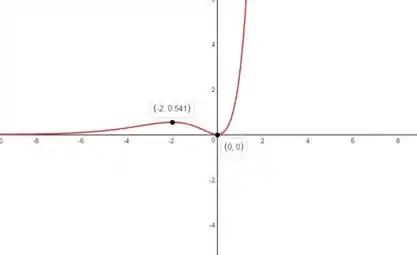
Resposta