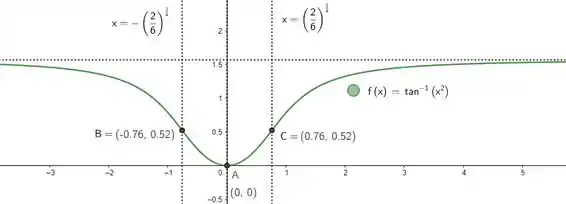
Seja a função dada por:
- Determine, caso existam, as equações das assíntotas horizontais do gráfico de
- Determine, caso existam, os intervalos onde é crescente
- Esboce o gráfico de . Marque em seu desenho as assíntotas horizontais e as abscissas dos pontos de máximo local e de mínimo local do gráfico de , caso existam.
- O gráfico de tem ponto de inflexão? Justique sua resposta.
Passo 1
Eu sei que funções trigonométricas e suas inversas são complicadas de trabalhar, mas relaxa meus caros, que a gente tira de letra. Quer ver? Dá uma olhada no círculo trigonométrico:

Quanto maior o arco então, maior o valor da tangente, não é? E quando:
Então:
Ok, mas e daí? Bem, como estamos procurando assíntotas horizontais, temos que fazer:
E olha só! Como o interior da função é um , qualquer sinal de negativo pra some! Logo:
Bem, queremos então o arco cuja tangente tende ao infinito. E já sabemos não é mesmo? Do círculo trigonométrico, tiramos que:
E essa vai ser a única assíntota horizontal! Em equação, temos:
Passo 2
Vamos ver agora quando essa função cresce e quando decresce. Pra isso, vamos precisar da primeira derivada, ok? Partiu derivar então:
Beleza, como a função vai crescer quando a primeira derivada for positiva e vai decrescer quando a primeira derivada for negativa, bora igualar à então, que aí achamos o ponto em que a derivada muda de sinal:
Show, agora vamos ver intervalos que envolvam essa única raíz de . Os intervalos são:
Pro primeiro intervalo, se usarmos, por exemplo, , temos:
E pro segundo intervalo, se usarmos, por exemplo, , temos:
Desses dois aí, só um dos intervalos vai ser de crescimento viu? A função cresce então em:
E no caso, vai decrescer no outro intervalo, .
Passo 3
Antes da gente partir pro esboço do gráfico, vamos dar uma olhada melhor no ponto que achamos no ponto anterior:
Não é que esse ponto é um ponto crítico? E como antes dele a função decresce e depois ela cresce, vai ser um ponto de mínimo! Ok, mas não acabamos com ainda! Saca só:
Opa, o ponto faz parte então da curva e está abaixo da assíntota, já que ela é:
E pra fechar com chave de ouro, vamos bater um papo sobre concavidade! Pra isso, vamos precisar derivar de novo! A segunda derivada de vai ser então:
Pra gente derivar esse cara aí, vamos precisar usar a regra do quociente, beleza? Vamos ter então:
E agora a gente iguala à ! Quando a segunda derivada for positiva, a concavidade tá pra cima. Quando for negativa, tá pra baixo. Simbora então:
Opa, duas raízes então. Vamos analisar o sinal da segunda derivada em intervalos que envolvam essas raízes então. Os intervalos vão ser:
Pro primeiro intervalo, vamos escolher, por exemplo, . Testanto então, temos:
Pro segundo intervalo, vamos escolher, por exemplo, . Testanto então, temos:
Pro terceiro intervalo, vamos escolher, por exemplo, . Testanto então, temos:
A concavidade então vai ser:
Sendo assim, temos tudo pra esboçar o gráfico! Ele vai ficar:
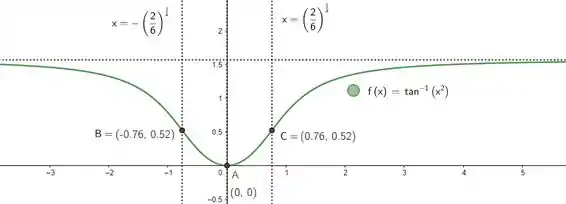
Passo 4
E pra fechar a questão e partir pro abraço, vamos falar dos pontos de inflexão de . Como os pontos de inflexão são exatamente os pontos em que a concavidade muda, vamos ter que:
E já achamos essas raízes em! Os pontos de inflexão vão ser então: