Seja :
Determine os intervalos de crescimento e de decrescimento de ;
Determine os pontos de máximos e mínimos locais de ;
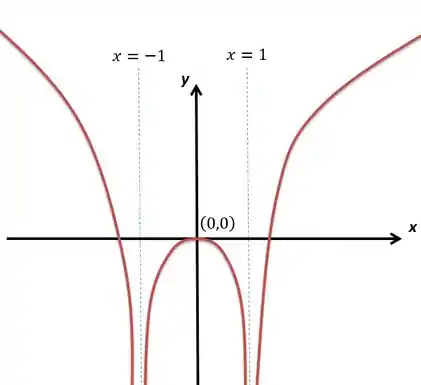
O gráfico da função é.
Passo 1
Vamos derivar o pela Regra da Cadeia:
Agora para analisar o crescimento e decrescimento de temos que observar o sinal da derivada, e isso nós podemos fazer através do quadro de sinais:
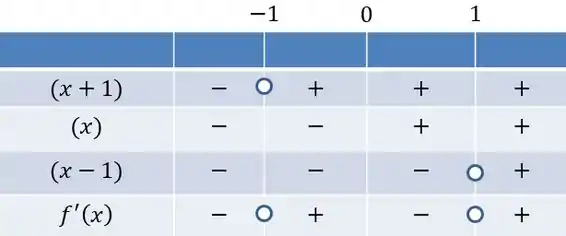
Concluímos com esse gráfico que a função é crescente apenas na região em que pertence ao intervalo de . é decrescente em .
Passo 2
Quando procuramos pontos de máximo ou de mínimo estamos em busca de onde a derivada é nula. Observando a nossa derivada, que achamos no item , vemos que isso só acontece quando . Para determinar se o ponto é de máximo ou de mínimo devemos observar o sinal da derivada antes e depois do ponto crítico em . Como temos no quadro dos sinais, a derivada é positiva antes e negativa depois, o que nos leva a pensar que gera um ponto de máximo local na função.
Passo 3
Para determinar o esboço da curva precisamos de outras informações: assíntotas, paridade da função e concavidade.Começamos procurando assíntotas:
As verticais ficam onde temos descontinuidades no domínio, ou seja, temos assíntotas verticais em e em :
Quanto às horizontais, vamos usar o limite da função quando vai para
Constatamos que não existem assíntotas horizontais pois os limites explodiram para .
Passo 4
Procurando agora assíntotas oblíquas, vamos pela definição modelar retas para a assíntota oblíqua por . Começamos buscando para :
O limite do jeito que está gera uma indeterminação , então vamos usar L’Hospital:
Passo 5
Sobre a paridade da função, basta substituir alguns pares de valores como e , e , e assim por diante, para reparar que a função é par, ou seja, .
Analisando agora a concavidade da função buscamos analisar o sinal da derivada segunda. Vamos achar a derivada de usando a Regra do Quociente:
Analisando o sinal do termo acima perceberemos que o termo do denominador, , é sempre positivo, bem como o . Isso significa que será sempre negativo, já que esse termo que é sempre positivo está multiplicando o , que é negativo. Concluímos, a concavidade é sempre para baixo.
Passo 6
Vamos reunir as informações que já temos:
- Domínio: ;
- função é crescente em . é decrescente em ;
- Ponto de máximo em ;
- Assíntotas verticais: e ; Assíntotas horizontais: ;
- Função par;
- Concavidade para baixo para todo ;
Somado a isso temos que as interseções com os eixos, onde e onde , se dão respectivamente em e em e . Vamos ao esboço: