UFCG – Cálculo Diferencial e Integral I – Atividade Avaliativa 3 (AV3) – Parte 1 – 2022.2 – Questão 3d.
- Seja a função , determine:
- Esboce o gráfico da função e determine a sua imagem.
Passo 1
Fala aí!!! Tudo belezinha com você? Bora desenvolver essa questão comigo?!
Bom, a questão dá pra gente a função
e pede para gente esboçar o gráfico da função e dizer qual a sua imagem. Certo? Então pensa comigo, qual a melhor maneira de esboçar o gráfico de uma função?
Bom, podemos fazer isso encontrando algumas informações importantes que ajudarão a gente a tornar o nosso trabalho mais simples. Primeiro, essa é uma função de terceiro grau, então o gráfico é uma cobrinha, podemos também encontrar suas raízes, assim saberemos em quais pontos ela corta o eixo , podemos olhar o crescimento e decrescimento dela, seus pontos de máximo e mínimo, e também sua concavidades. Tudo isso vai fazer como que a gente seja capaz de desenhar o gráfico perfeito. E tudo isso já foi encontrado nos itens anteriores.
Então vamos juntar todas as informações e colocar aqui.
Passo 2
O domínio da nossa função é igual todos os reais, já que é uma função polinomial
Igualando nossa função a zero, encontramos as raízes iguais a:
Raízes e
E o seu comportamento é:
E temos o seguinte comportamento:
ponto de inflexão.
tem concavidade voltada para cima.
tem concavidade voltada para baixo.
E juntando tudo isso, ficamos com o esboço do gráfico na função da seguinte forma:
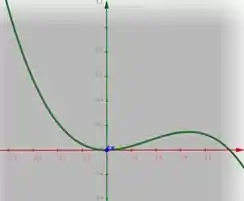
E pra fechar, podemos ver que a imagem são todos os valores reais, já que pode assumir qualquer valor.
E prontinho. Problema resolvido. 😊
Partiu próxima?!
Resposta
No desenvolvimento.