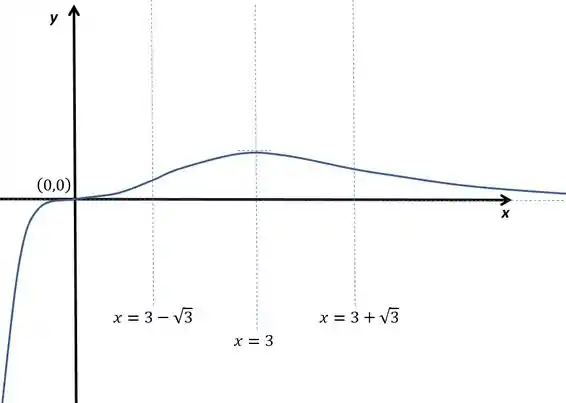
Esboce o gráfico de , determinando o seu domínio, os intervalos de crescimento e de decrescimento, concavidades e assíntotas (caso existam).
Passo 1
Assim como o cara pediu no enunciado nós temos que dividir a análise do gráfico em domínio, análise do crescimento, análise de concavidade e assíntotas. Começamos no domínio:
Como a gente vê, não há fator limitante para o domínio. Nosso domínio vai ser:
Passo 2
Vamos observar o crescimento da função; para isso analisamos o sinal da derivada primeira. Vamos derivar o termo pela Regra do Produto:
Como a exponencial e o são sempre positivos nós vemos que o sinal da derivada só depende de . Com isso, a função é decrescente em e crescente em .
Sobre pontos críticos, um apenas, em . Como o termo é positivo antes e negativo depois, esse é um ponto de máximo, não havendo pontos de mínimo.
Passo 3
Vamos olhar a derivada segunda agora e a concavidade. Vamos, novamente pela Regra do Produto:
Vamos procurar as raízes dessa parábola que apareceu:
Ou seja, a derivada segunda será:
O sinal do vai depender de todos os termos que temos ali, menos a exponencial. Com isso, vamos observar concavidade com o quadro de sinais:
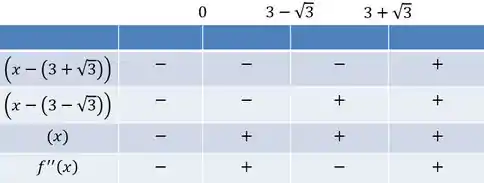
A gente vai reparar que a concavidade é para cima quando e para baixo quando está em .
Ponto de inflexão em , e .
Passo 4
Assíntotas agora. As verticais estão relacionadas com as descontinuidades, ou seja, não teremos nenhuma delas para essa função.
Para assíntotas horizontais temos que lançar o limite para e :
Uma assíntota horizontal em . Ainda podemos ter uma assíntota oblíqua em , vamos tentar:
Vemos que também não teremos assíntotas oblíquas
Passo 5
Agora reunimos as informações que já achamos:
Vamos para o esboço, sendo e :