Considere a função:
Cujas derivadas primeira e segunda são, respectivamente:
- O domínio da função;
- As assíntotas horizontais e verticais, caso existam;
- Os intervalos onde a função é crescente e decrescente;
- Os valores máximo e mínimo locais e/ou globais caso existam;
- Os intervalos onde a concavidade é para cima, onde é para baixo e os pontos de inflexão;
- Utilizando as informações adquiridas esboce um gráfico de .
Passo 1
Encontremos o domínio então. Quais valores pode assumir de forma que não vai dar nenhuma coisa do tipo , ou ? Precisamos garantir que aquele denominador não vai dar zero. Aqui vale a observação de não tem problema o termo da raiz ser negativo, já que ela é cúbica. Portanto:
Segue que:
Passo 2
As assíntotas horizontais saem pelos limites abaixo:
Pondo em evidência pra fora da raiz cúbica:
Mesma coisa com o outro:
Ou seja, não tem assíntotas horizontais.
Já as verticais, vamos pelo limite pra bagunçar esse denominador:
Portanto uma assíntota vertical é . Se considerarmos o ponto , temos a mesma situação:
Assim, temos outra assíntota vertical em .
Passo 3
Os intervalos onde a função é crescente são aqueles onde a derivada é positiva:
E decrescente onde ela é negativa:
Portanto:
Façamos, então, análise do sinal. Quais fatores influenciam no sinal? Aqueles que não tem expoente par. Por exemplo, o fator no denominador não influencia, já que é sempre positivo. Portanto, resta analisar :
Mesma coisa com o intervalo onde é decrescente:
Com o detalhe que os pontos em que não fazem parte do domínio, portanto os intervalos são:
Passo 4
Os máximos e mínimos ocorrem onde a derivada é igual a zero:
Agora a questão é analisar a troca de sinal em torno desses pontos. Em temos que a derivada é negativa antes e positiva depois, portanto é um ponto de mínimo.
Em a derivada é positiva antes e negativa depois, portanto é um ponto de máximo.
Como com o a função também tende para e , não há máximo nem mínimo globais. Ambos são locais.
Passo 5
Os intervalos da concavidade correspondem ao sinal da derivada segunda:
Infelizmente agora toda uma série de funções vão entrar na nossa análise. Vamos precisar recorrer à nossa tabelinha da marotagem. As funções no caso são essas três:
Destrinchando melhor, pra ficar mais fácil, temos:
Portanto, acredito que fique melhor escrever assim:
Seus zeros são:
E é em torno deles que vamos construir nossa tabela. Segue:
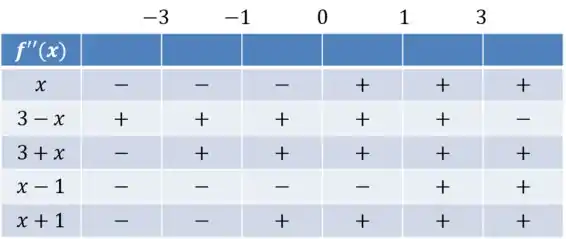 Multiplicando os sinais, chegamos ao sinal da derivada segunda:
Multiplicando os sinais, chegamos ao sinal da derivada segunda:
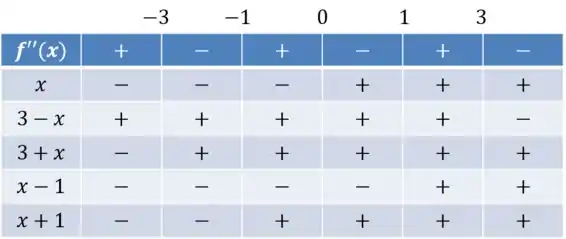 Portanto, a concavidade é para cima em:
Portanto, a concavidade é para cima em:
E para baixo em:
E os pontos de inflexão são:
Passo 6
Obtemos o gráfico:
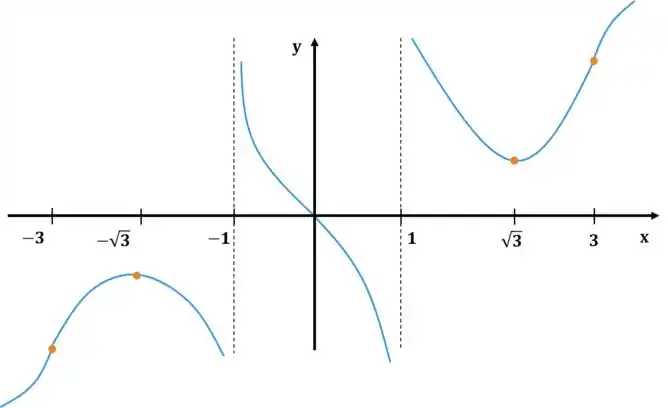
Resposta
Ei, a resposta está no passo a passo :)