UFABC – Cálculo 1 – Lista 1 – 5d
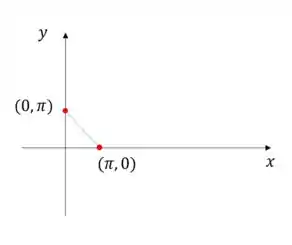
Escreva a equação da reta tangente às curvas no ponto especificado. Esboce o gráfico de e da reta tangente.
Passo 1
E aí, gente!! Tudo bem? Vamos para mais um desafioo!?
O primeiro passo aqui é a gente lembrar da equação da reta tangente!!!
Onde é o ponto de interesse nosso que foi dado no problema!
Então olhando pra equação da reta tangente, o que a gente vai precisar encontrar? Bem, primeiro precisamos calcular e depois .
Para calcular a gente vai precisar pegar nossa , em outras palavras, uma vez que o enunciado nos deu a função e conhecemos o ponto desejado, conseguimos calcular tranquilamente o valor de , certo?
Passo 2
Vamos calcular quem será nosso quando
Show!! Agora partiu calcular a derivada da e depois substituir o valor de por 2!
Para essa derivada, vamos precisar lembrar sobre a seguinte propriedade:
Aplicando a regra do quociente, temos;
Substituindo agora
Passo 3
Usando a equação da reta:
Passo 4
Para a construção do gráfico de uma reta, podemos conhecer dois pontos e depois ligar os mesmos. Então, por exemplo, um bom ponto pra partirmos é ver qual valor assumirá quando .
Logo, temos o par
Agora quando , qual será o valor de ?
Logo, temos: .
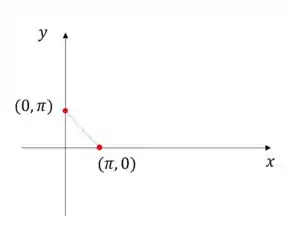
Resposta
