4. Esboce o gráfico da função , indicando:
- Interseções com os eixos coordenados;
- Regiões de crescimento e decrescimento, máximos e mínimos locais;
- Regiões de concavidade para baixo e para cima e pontos de inflexão;
- Comportamento no infinito e assíntotas;
- Máximo e mínimo absoluto.
Passo 1
Oi, galerinha! Tudo bom? Aqui nós temos que esboçar o gráfico da função
E os passos para fazer esse esboço são justamente os comandos pedidos em cada item. Então vamos fazer o que o problema nos pede em cada item e fazer esse gráfico!
Passo 2
- A gente começa encontrando os pontos onde o gráfico corta o eixo e . Ou seja, vamos encontrar os pontos onde e .
- Agora vamos encontrar os pontos de máximo e mínimo da função. Esses pontos são chamados pontos críticos.
- Pelo desenho acima, já conseguimos ver que temos uma concavidade para baixo no ponto .
- Agora vamos avaliar as assíntotas horizontais e verticais.
- Por fim, temos que verificar quais são so máximos e mínimos absolutos. Mas isso, nós já fizemos. Vimos que a função só possui um ponto de máximo, então temos um máximo absoluto em .
Começando por ,
Ou seja, o gráfico corta o eixo no ponto .
Para , teremos
Como o termo nunca poderá ser zero, pois é uma exponencial. Para essa igualdade ser verdade temos que apenas pode zerar. Logo
Ou seja, o gráfico ira cortar o eixo no ponto .
Passo 3
Para encontrar um ponto crítico, temos que descobrir quais pontos que a nossa derivada é igual a zero. Ou seja, temos que fazer,
Temos a seguinte função,
Derivando a nossa função, aplicando a regra do produto, ficamos com
Igualando a zero, ficamos com
Como o termo nunca poderá ser zero, pois é uma exponencial. Para essa igualdade ser verdade temos que apenas pode zerar. Logo
Ou seja, o ponto é um ponto crítico.
Agora vamos fazer os testes de crescimento e decrescimento!
Passo 4
Basicamente, o que temos que fazer agora é a avaliar a derivada antes e depois.
Se a derivada for positiva temos que a função será crescente (ou seja, vai para cima), caso ela seja negativa, a função é decrescente (ou seja, vai para baixo).
Vamos montar então o quadro dos sinais. Lembrando que a nossa derivada é:
Com isso, ficamos

Analisando os valores obtidos na primeira linha, ficamos com

Já para a segunda linha, teremos valores negativos para números que e valores positivos para números menores que .
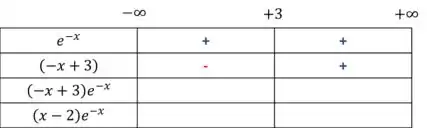
Multiplicando a primeira e segunda linha para chegarmos na nossa derivada, ficamos com
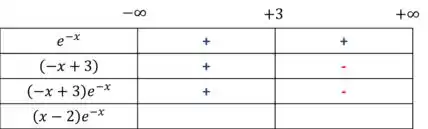
Agora que sabemos quando a derivada é positiva e negativa, sabemos quando ela cresce ou decresce,
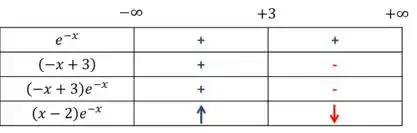
Ou seja, ela cresce para valores menores que e volta a decrescer para valores maiores que . Ao desenharmos isso, encontramos um ponto de mínimo.

Passo 5
Mas para avaliarmos as concavidades e pontos de inflexões possiveis, precisamos fazer o teste da segunda derivada.
Tinhamos a seguinte derivada,
Derivando de novo (também aplicando a regra do produto),
Agora temos que avaliar o sinal: se a temos uma concavidade para baixo; se temos uma concavidade para cima; e se temos um ponto de inflexão.
Avaliando o ponto crítico , teremos,
Ou seja, temos uma concavidade para baixo.
Agora vamos verificar se tem um ponto de inflexão, fazendo .
Como o termo nunca poderá ser zero, pois é uma exponencial. Para essa igualdade ser verdade temos que apenas pode zerar. Logo
Ou seja, o ponto é um ponto de inflexão.
Passo 6
Para encontrar as assíntotas horizontais, avaliar quando
Repara que caímos em uma interminação do tipo . Então vamos aplicar L’Hoptal para resolver esse limite.
Derivando em cima e embaixo ficamos com
Ou seja, temos uma assíntota horizontal em .
Agora vamos avaliar
Ou seja, não temos assíntotas horizontais para quando .
Para as assíntotas verticais, temos que verificar os pontos onde a função não existe. Por exemplo, o domínio de são apenas os números maiores que zero. Já o domínio a parte são todos reais. Logo, o domínio da função são todos os números reais. Sendo assim, não há assíntotas verticais.
Passo 7
Agora se analisarmos o comportamento da função para quando ela se aproxima de , vamos tendo valores cada vez mais negativos. Deste modo, não há mínimo absoluto.
Passo 3
Por fim, juntando todas a informações que obtivemos sobre a função, podemos esboçar o seguinte gráfico.
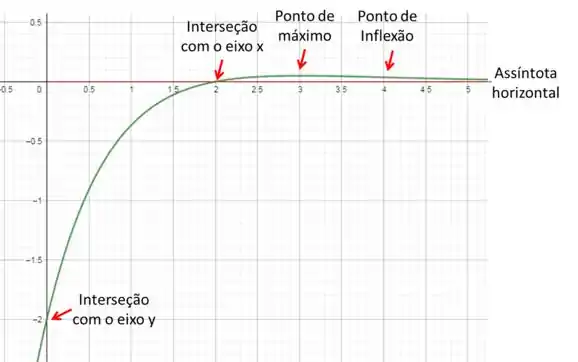
Resposta
No texto.