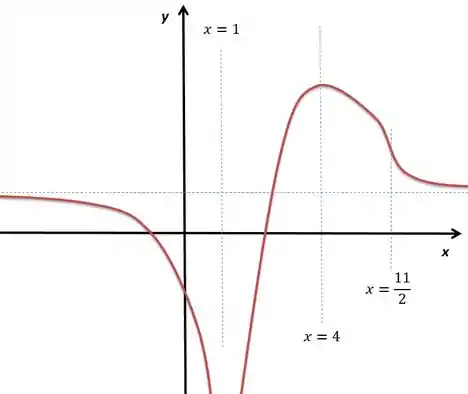
Esboce o gráfico de , determinando o seu domínio, os intervalos de crescimento e decrescimento, a concavidade e calculando todos os limites necessários.
Passo 1
Assim como o cara pediu no enunciado nós temos que dividir a análise do gráfico em domínio, análise do crescimento, análise de concavidade e assíntotas. Começamos no domínio:
Como a gente vê, o único fator limitante é o denominador da função, que não pode ser . Para isso, deve ser sempre diferente de . Nosso domínio vai ser:
Passo 2
Vamos observar o crescimento da função; para isso analisamos o sinal da derivada primeira. Vamos derivar o termo pela Regra do Quociente e da Cadeia:
Como a gente vê, o sinal só depende de e do . Vamos fazer o quadro de sinais para diversos intervalos:
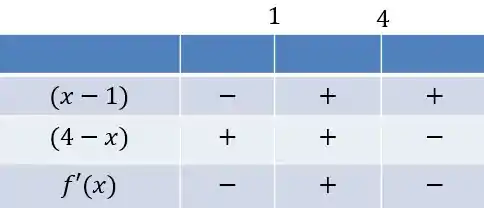
Como dá para ver, a .
Sobre pontos críticos, temos dois, e . Porém, não está definido no domínio, então não será ponto de máximo ou mínimo. Agora, será, sendo que sua derivada é positiva antes e negativa depois, consistindo num ponto de máximo local.
Passo 3
Vamos olhar a derivada segunda agora e a concavidade. Vamos, novamente pela Regra do Quociente e da Cadeia:
O sinal do não vai depender do denominador, que está elevada a um expoente par. Só depende de , que é positivo para e negativo para .
A gente vai reparar que a concavidade é para cima quando e para baixo quando está em .
Ponto de inflexão em .
Passo 4
Assíntotas agora. As verticais estão relacionadas com as descontinuidades, ou seja, vamos fazer o limite para e :
Assíntota vertical em .
Para assíntotas horizontais temos que lançar o limite para e :
Assíntota horizontal em .
Não existem assíntotas oblíquas já que encontramos assíntotas horizontais para direita e para esquerda.
Passo 5
Agora reunimos as informações que já achamos:
Vamos para o esboço, sendo , e :