Considere a função dada por:
- Determine, caso exista(m), o(s) intervalo(s) de crescimento e decrescimento de .
- Determine, caso exista(m), o(s) intervalo(s) onde o gráfico de tem concavidade voltada para cima e onde tem concavidade voltada para baixo.
- Faça um esboço do gráfico de indicando explicitamente o(s) ponto(s) de máximo, de mínimo e de inflexão. Esboce também a(s) reta(s) tangente(s) ao gráfico de no(s) ponto(s) em que a derivada é zero e no(s) ponto(s) de inflexão.
Passo 1
Cara, como precisamos avaliar crescimento ou decrescimento, o que devemos fazer é avaliar o sinal da primeira derivada, afinal de contas...
Então bora derivar !
Passo 2
Derivando...
Agora é só analisar o sinal dessa função derivada... Como estamos falando da função seno, seu gráfico é a senoide, com período :
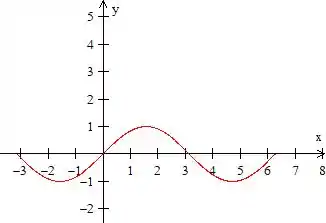
Mas... estamos falando de um deslocamento em de uma unidade pra cima, afinal a função derivada é o seno somado com ...
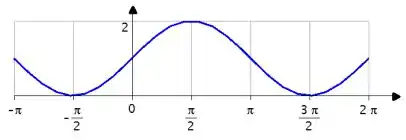
Perceba, que como o seno é no máximo , a função derivada em alguns pontos, mas ela é sempre maior ou igual a , então a função cresce no intervalo de , mas não decresce.
Passo 3
Analisar concavidades é outra análise de sinal, mas dessa vez da segunda derivada...
Derivando a primeira derivada...
O gráfico do cosseno também é um gráfico bem conhecido. Passa por quando é e tem o período também de ...
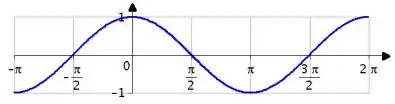
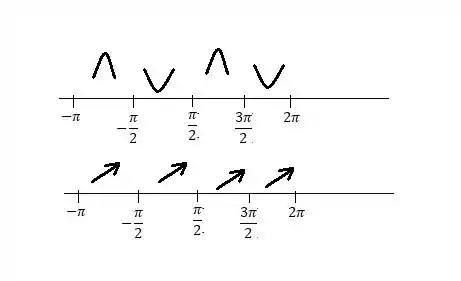
Repare no gráfico do cosseno que ele tem intervalos positivos e negativos... Então:
De a e também de até , a concavidade é pra cima, enquanto que nos outros intervalos, onde , a concavidade é para baixo.
Passo 4
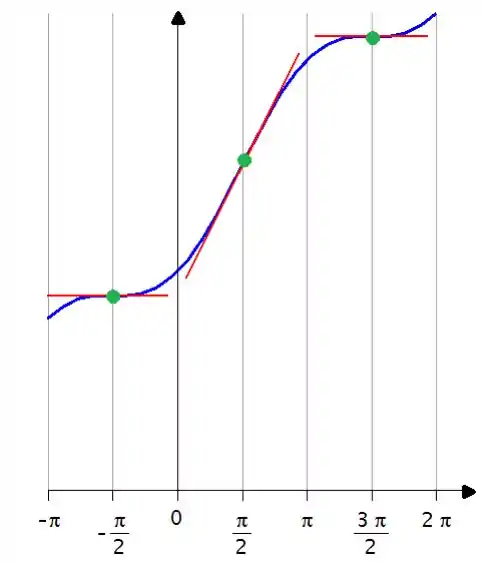
Para esboçar o gráfico, vãos reunir todas as informações até agora:
- Sabemos que a função é inteiramente crescente no intervalo de a , e que a derivada zera nos pontos onde o gráfico da primeira derivada encosta no eixo ...
- Quanto a concavidade...
Então a curva tem mais ou menos esse aspecto...
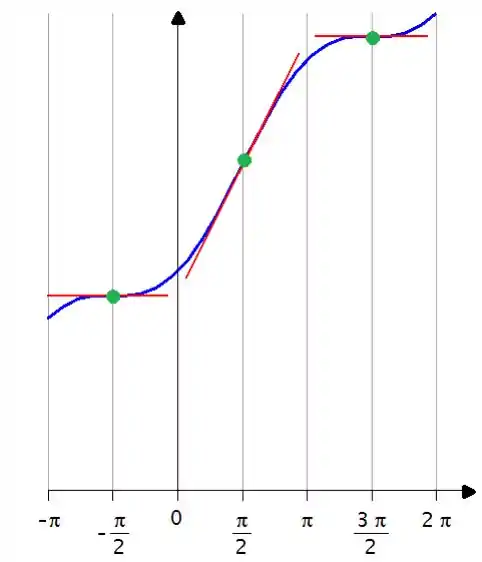
Resposta
Função é crescente de