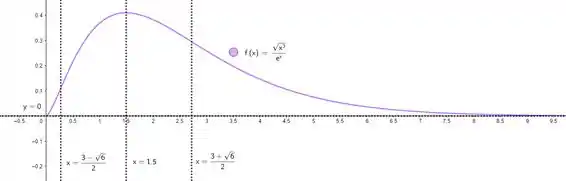
Considere a função:
Cujas derivadas primeira e segunda são, respectivamente:
- O domínio da função;
- As assíntotas horizontais e verticais, caso existam;
- Os intervalos onde a função é crescente e decrescente;
- Os valores máximo e mínimo locais e/ou globais caso existam;
- Os intervalos onde a concavidade é para cima, onde é para baixo e os pontos de inflexão;
- Utilizando as informações adquiridas esboce um gráfico de .
Passo 1
Encontremos o domínio então. Quais valores pode assumir de forma que não vai dar nenhuma coisa do tipo , ou ? Precisamos garantir que aquele denominador não vai dar zero. Mas como é uma função que nunca zera, então podemos escolher qualquer valor de .
Mas não para por aí: ainda temos a raiz quadrada do denominador! Se eu escolher um número negativo qualquer, o denominador “tá de boas” mas o numerador vai dar uma coisa estranha tipo ou e isso não pode! Bem, já que é assim, vamos ter então que o domínio vai ser:
Passo 2
As assíntotas horizontais saem pelos limites abaixo:
Como essa função já não tá definida mesmo pra , só precisamos nos preocupar com o primeiro limite. Fazendo ele obtemos:
E não é que é algo que podemos tirar por L’Hospital? Então vamo que vamo:
Ok, se fizemos o limite de continuamos com . Mas isso n tem problema algum, só realizar L’Hospital de novo. Aí ficamos com:
Opa, agora as coisas mudaram! Aplicando o limite vamos ter:
Então sim, temos uma assíntota horizontal e ela vai ser
Já as assíntotas verticais, o normal seria a gente fazer limites tendendo à valores que baguncem com o denominador ou numerador, gerando indeterminações. Mas como já vimos que a função está definida em , não tem nenhum valor candidato pra gente checar.
Poderíamos até tentar fazer mas nem o primeiro valor do domínio gera indeterminação, saca só:
Pois é, sem assíntotas verticais dessa vez. No entanto, pra esboçar o gráfico lá na frente, guarda o que acabou de ver, que .
Passo 3
Os intervalos onde a função é crescente são aqueles onde a derivada é positiva:
E decrescente onde ela é negativa:
Portanto:
Pra gente saber quando ela é positiva e quando é negativa vamos ter que ver o sinal em intervalos que envolvam alguns pontos interessantes. Esses pontos nada mais vão ser do que os pontos que a primeira derivada zera e os pontos que ela não existe!
Beleza, então vamos nessa
Mas não vale porque se escolhêssemos esse valor e calculássemos , iríamos achar uma indeterminação! Então temos só uma raiz pra primeira derivada:
Agora, os pontos em que a derivada não existe são os que fazem:
Beleeeza, então os intervalos tem que ser montados usando os pontos e . Vamos ter então esses três:
Opa, uma macete aqui cai bem: como a gente já sabe que a função não está definida pra , já descartamos logo. Então pro segundo intervalo, vamos ver, por exemplo, . Vamos ter:
E pro segundo intervalo, vamos usar, por exemplo, . Vamos ter
Os intervalos de crescimento e decrescimento vão ser então
Passo 4
Os máximos e mínimos ocorrem onde a derivada é igual a zero.
Agora a questão é analisar a troca de sinal em torno desses pontos. Em , antes da raiz temos que a derivada é positiva e em , ponto depois da raiz, a derivada é negativa. Portanto, estamos olhando na verdade pra um ponto de máximo.
Como com o a função também tende para , esse ponto de máximo é na verdade um ponto e máximo global!
Passo 5
Os intervalos da concavidade correspondem ao sinal da derivada segunda:
E aí precisamos fazer a mesma coisa: ver pontos em que a segunda derivada zera e pontos em que ela não existe. Só de olhar pro denominador, vemos que:
Então é um dos pontos. Guarda ele aí. Agora, quais pontos zeram, temos que fazer:
O que é verdade quando e/ou quando . No segundo caso, a resposta sai por Bhaskara. Então simbora:
E como a função não está definida mesmo pra , os intervalos que vamos analisar vão ser:
Como:
Pra testar o primeiro intervalo, vamos usar, por exemplo, . Vamos ter:
Pro segundo intervalo, vamos usar, por exemplo, . Vamos ter:
E pro último intervalo, vamos usar, por exemplo, . Vamos ter:
Como a concavidade é pra cima quando a segunda derivada é positiva e pra baixo quando ela é negativa, temos então que ela vai ser pra cima nos intervalos
E para baixo em:
E os pontos de inflexão são:
Passo 6
Obtemos o gráfico:
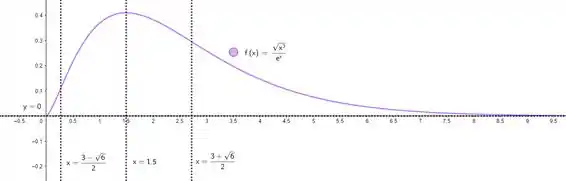
Resposta
- Única assíntota é horizontal:
- é um ponto de máximo global