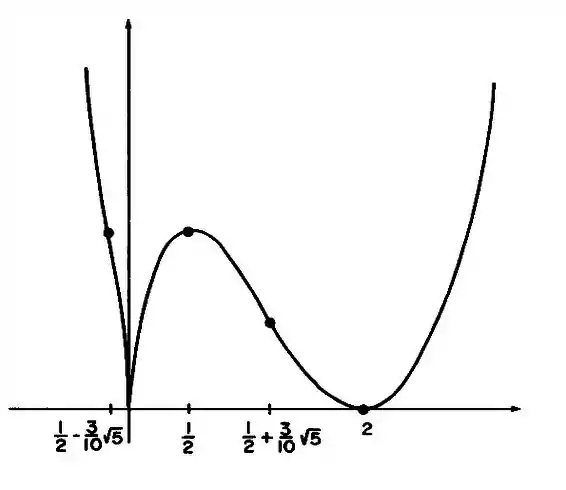
Considere a função dada por
- Determine os intervalos onde é crescente e onde é decrescente. Determine os pontos de máximo e de mínimo locais de .
- Determine os intervalos onde possui concavidade para cima e também onde possui concavidade para baixo. Determine os pontos de inflexão de .
- Calcule os limites pertinentes a existência de assíntotas.
- Esboce o gráfico de
Passo 1
Através da regra do produto e cadeia, obtemos:
A função é crescente quando a primeira derivada é positiva e decrescente quando contrário. Então precisamos analisar o sinal da derivada, para isso, vamos montar um quadro de sinais bem bonito com os as partes de que trocam de sinal. Essas partes só poderão trocar de sinal ao passar pelas raízes, então determinemos:
Assim, testamos para cada região entre esses pontos:
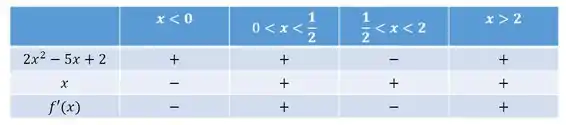
Assim, a função é crescente para cima para e . É decrescente para baixo para e .
Os pontos de zeros e indeterminação da derivada também serão os pontos críticos. Pelo teste da primeira derivada, vemos que esta era negativa a esquerda de e positiva à direita, então trata-se de um ponto de mínimo, assim como em . Do contrário, concluímos também que é um ponto de máximo.
Passo 2
Pela regra do quociente, obtemos:
A função é côncava para cima quando a segunda derivada é positiva e será côncava para baixa do contrário. Então, temos que analisar o sinal da segunda derivada. Como todos os outros termos são sempre positivos, o sinal vai depender somente do polinômio de segundo grau:
Que tem raízes:
Testando nas regiões entre esses pontos obtemos:

Assim, a função é côncava para cima para e e côncava para baixo em .
Nos pontos em que ocorre troca de concavidade, temos os pontos de inflexão, ou seja, em:
Passo 3
Calculando o limite no infinito para determinar as assíntotas horizontais:
Logo, não há assíntota horizontal.
Não há ponto de indeterminação, e, portanto também não haverá assíntota vertical.
Quanto às assíntotas obliquas:
Portanto, não há qualquer assíntota.
Passo 4
Com os resultados obtidos, chegamos ao seguinte esboço:
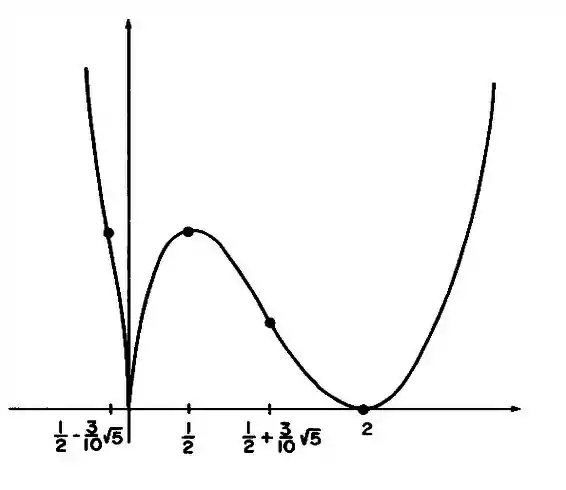
Resposta