Considere a função dada por
- Encontre, caso existam, as assíntotas verticais de .
- Determine os pontos críticos de , intervalos onde a função é crescente e onde a função é decrescente.
- Encontre os extremos relativos e absolutos de , caso existam.
- Mostre que é côncava para cima.
- Esboce o gráfico de .
Passo 1
(a)
Está bem, temos uma questão de esboço aqui, vamos letra por letra. Começando pela letra , vamos determinar as assíntotas verticais da função. Essas assíntotas ocorrem nos pontos onde a função não está definida.
Como precisamos que o que esteja dentro do log seja sempre positivo, então temos que:
Como o termo ao quadrado é sempre zero ou positivo, isso será verdade para . Assim, vamos calcular o limite neste ponto. Pela direita e esquerda
De maneira semelhante:
Como o limite não existe nesse ponto, temos uma assíntota vertical aqui.
Passo 2
Vamos para a letra agora. Para determinar os pontos críticos, que ocorrem quando a derivada é zero ou não existe, e os intervalos de crescimento e decrescimento precisamos derivar a função. Então vamos lá:
Para facilitar nossa vida, usamos a propriedade: e deixamos:
A derivada não existe quando o denominador zera, em . E será zero quando o numerador for zero, neste caso. Quando . Assim, os pontos críticos são:
Vamos analisar o crescimento agora. Para tal, analisamos o sinal do numerador e denominador e fazemos um quadro de sinais, marcando os pontos onde o sinal muda.

Pela tabela, a função cresce para e e decresce para .
Passo 3
(c)
Vamos agora determinar os extremos. Temos e como pontos críticos. Voltando a tabela lá do passo anterior, vemos que a derivada é menor que zero à esquerda de e maior que zero à direita desse ponto. Dessa maneira, pelo teste da primeira derivada, esse é um ponto de mínimo.
Para , desconsideramos, pois já vimos que temos uma assíntota ali. Para verificar se o ponto que achamos é mínimo global, vamos aplicar o limite:
Ou seja, existem valores menores que esse mínimo e ele será, portanto, apenas local. Nem precisamos calcular o limite para .
Passo 4
Vamos ver agora a letra . Será que a função é côncava para cima sempre? Para saber, vamos derivar novamente. Pela regra do quociente:
Portanto é sim, sempre côncava para cima.
Passo 5
Agora finalmente, a letra . A partir dos dados obtidos em cada um dos itens, chegamos ao gráfico:
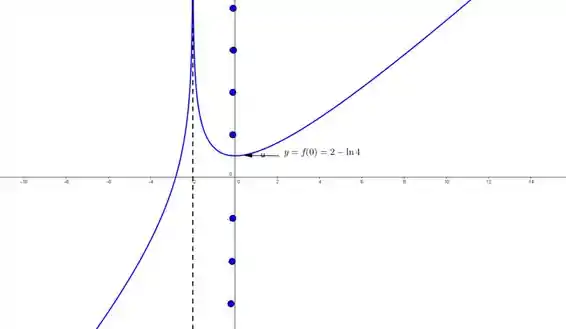
Que tem assíntota vertical em , indo para infinito à esquerda e à direita, como mostrou:
Que cresce para e e decresce para e tem mínimo em . Além disso, a função vai para menos e mais infinito nos extremos esquerdo e direito, respectivamente, conforme vimos no passo .
Resposta
- Assíntota vertical em .
- A função cresce para e e decresce para . Pontos críticos em e .
- Mínimo local em .
- .