Um gato pula em um carrossel que está descrevendo um movimento circular uniforme. No instante a velocidade do gato é , medida em um sistema de coordenadas horizontal. No instante a velocidade é Quais são:
- o módulo da aceleração centrípeta do gato.
- a aceleração média do gato no intervalo de tempo , que é menor que um período.
Passo 1
Vamos lá, galera!
Como ele nos diz que temos um MCU, no tempo e no tempo teremos as velocidades e o vetor posição , como mostrado abaixo.
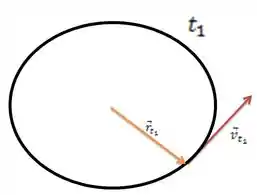
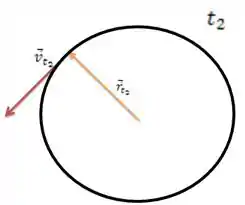
Passo 2
Mas se liga só, ele nos pede o módulo da aceleração centrípeta.
Lembra aí como se calcula? Saca só!
Mas quem seria o nosso
Justamente o módulo da velocidade nos dois casos, que nada mais nada menos é que:
Desta forma, teremos...
Passo 3
Mas pera aí! Ele não falou o , daí a conta não sai!
![]()
Calma! É só lembrar que, . Mas aí também temos que .
Daí, teremos que:
Mas e aí? Não temos o !
Aí que vem o pulo do gato!

Lembra dos vetores posição lá da nossa primeira figura. Dizendo que ele fez o percurso entre e , teremos o seguinte caso:
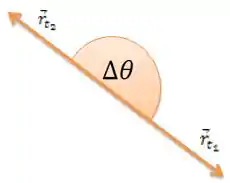
E o nosso será .
Passo 4
Assim, vamos ter que:
Agora, tacando lá na fórmula do Passo 2, teremos:
Passo 5
b)
Pela definição de aceleração média, teremos que:
Calculando o módulo da aceleração, teremos:
Resposta
a)
b)