UFSCAR, Sem Campus, Física 1, AV3 - 2021.2 - Prof° Raphael Santarelli, Questão 2a
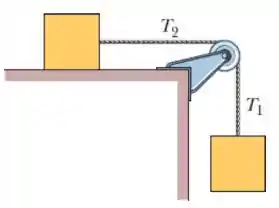
Na figura abaixo dois blocos de mesma massa estão ligados por uma corda de massa desprezível, que passa por uma polia em formato de disco com raio e massa . A corda não escorrega na polia, e não há atrito no eixo da polia. Porém, existe atrito cinético entre a mesa e o bloco que escorrega. Quando o sistema é liberado a partir do repouso, a polia gira de em , e a aceleração dos blocos e da polia são constantes.
Qual a aceleração angular da polia? Ela é positiva ou negativa?
Passo 1
Eaí galera, tudo bom com vocês?
Então, nessa questão temos dois blocos ligados por uma corda, que passa por uma polia. A grande diferença aqui é que essa polia não é ideal (de massa desprezível), mas ela possui massa . Enquanto os blocos possuem massa de Também é falado que o raio da polia vale .
O enunciado nos diz que o sistema é liberado do repouso e que em a polia girou . E, por fim, algo bem importante é que as acelerações do bloco e da polia são constantes.
A partir dessas informações precisamos determinar a aceleração angular da polia, bem como se ela é positiva ou negativa.
Bom, como a polia possui aceleração constante podemos usar uma das equações do movimento circular uniformemente variado:
Massa! Bora aplicar essa ideia então!
Passo 2
Foi falado que em a polia girou . Assim, temos:
Além disso, como o sistema parte do repouso, temos também que:
Assim, aplicando na equação que comentamos no passo anterior vamos ter:
Isolando , temos:
Além disso, como o sistema de blocos se movimenta para baixo (pela ação da gravidade), a polia deve girar no sentido horário (que convencionaremos como o sentido positivo de rotação, beleza?).
Então é isso gente, terminamos esse item!
Muito obrigado pela atenção 😉
Resposta
(sentido horário: positivo)