Uma partícula descreve um movimento circular, com velocidade de módulo constante e igual a . Num intervalo de tempo em que percorre da circunferência, o módulo de seu vetor velocidade média é igual a
Passo 1
Os dados do enunciado são
O vetor velocidade média é
Vamos fazer um esboço do movimento, considerando o raio do movimento .
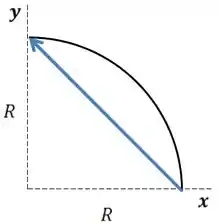
Vamos considerar que o corpo está girando no sentido anti-horário.
Passo 2
O vetor em azul, é o vetor deslocamento, como ele quer o módulo do vetor velocidade média devemos ter o módulo do vetor deslocamento.
Passo 3
Então
Porém, não temos nenhuma dessas variáveis.
Passo 4
Sabemos que o módulo da velocidade é ,
Como a velocidade é constante
Onde é a distancia percorrida, que nesse caso é do comprimento do círculo de raio .
O comprimento de um circulo completo é então
Passo 5
Substituindo na equação do módulo da velocidade média
- ''Resposta
Letra A