Uma partícula descreve um movimento circular de raio , com velocidade de módulo constante e igual a . Num intervalo de tempo em que percorre da circunferência, o módulo de seu vetor aceleração média é

1. ;
2. ;
3. ;
4. ;
5. ;

Vamos fazer um esboço de como é esse movimento, como ele está com um movimento circular a velocidade é tangente ao círculo.]

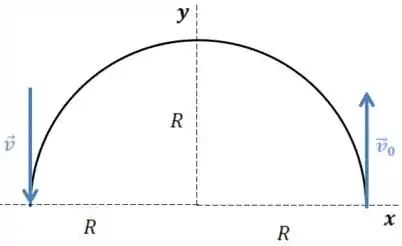
Repare que, sabendo que o módulo das velocidades é ,

Uma está apontando para cima, logo positiva, enquanto outra está apontando para baixo, logo negativa.

Voltando a fórmula do vetor aceleração média

O módulo do vetor aceleração media é

Porém não temos

Sabemos que o módulo da velocidade é ,

Como a velocidade é constante

Onde é a distancia percorrida, que nesse caso é do comprimento do círculo de raio .

O comprimento de um circulo completo é então

Queremos , então

Substituindo na fórmula do módulo da aceleração vetorial