Considere uma serra circular movida por um motor. O centro do disco da serra, quando a mesma é usada para cortar madeira, fica submetido a um torque cujo módulo vale . Se, nesta situação, tal disco gira com uma velocidade angular constante de , o trabalho realizado pelo motor em vale:
Passo 1
Bem, para a gente começar e começar bem o nosso problema, vamos dar uma desenhada no que está acontecendo, pode ser?
Temos um disco de uma cerra girando e batendo numa madeira para cerrá-la. O disco tem certo raio :
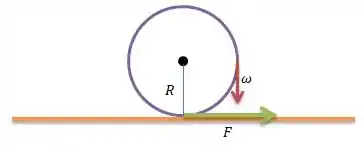
Repare que quando o disco bate na madeira, surge uma força no disco que é contra a velocidade de rotação dele. Essa força vezes o raio é a força que gera o torque de no centro de rotação:
Beleza, mas queremos o trabalho feito pelo disco ao cortar a madeira, e como a gente pode encontrar isso?
Trabalho... Tenha em mente que será sempre...
Onde representa p deslocamento. O que vamos ter que fazer agora, é trabalhar com essa fórmula aí! Preparado?
Passo 2
Pow! Sabemos que o deslocamento pode ser dado pela velocidade tangencial vezes o tempo de trabalho...
Então, o trabalho será...
Além disso, quando um disco está girando com velocidade angular , podemos associar a velocidade tangencial com a velocidade angular por...
Então...
Só que o que vem a ser ?
SIM! O torque que já comentamos sobre!
Passo 3
Então agora, meu amigo, é só substituir! Lembre-se que a velocidade angular é nesse caso, e também não se esqueça de que queremos o trabalho em , portanto, ...
Resposta
Letra E.