Exercícios Resolvidos de Velocidade e Aceleração Médias no Movimento Circular

Ver Teoria

Exercício 58 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 59 60 61 62 63 64 65

Enunciado

USP, Sem Campus, Física 1, Coletânea de Exercícios - Parte II - Colisões, Torque, Cinemática Angular, Questão 29b

Uma bolinha presa a um fio de massa desprezível gira em torno de um eixo vertical com velocidade escalar constante, mantendo-se a uma distância do eixo; o ângulo é igual a . O fio passa sem atrito através de um orifício numa placa, e é puxado lentamente para cima até que o ângulo passa a .

Qual foi a variação da velocidade de rotação?

Passo 1

Eaew, tudo bem?

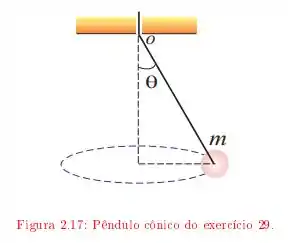
O enunciado descreve o seguinte esquema

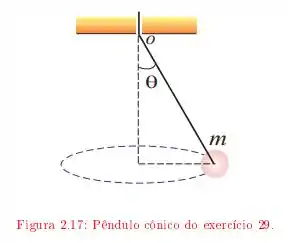
a bolinha de massa gira com velocidade escalar constante ao longo de uma circunferência. O ângulo é igual a quando a distância entre o eixo e a bolinha é , se puxarmos o fio aumentamos o ângulo para , sabendo isso queremos saber

Qual foi a variação da velocidade de rotação?

Na última alternativa nós obtivemos a relação

e como temos que , podemos usar essa relação para obter o que se pede na alternativa! Bora lá!

Passo 2

Dividindo ambas as relações em nossa expressão temos que

ou seja, podemos calcular a razão entre as velocidades como

A questão foi isso! Te vejo na próxima! Tchau Tchau!

Resposta

Exercícios de Livros Relacionados

Pulsares são estrelas de nêutrons que emitem raios X e outras radiações de tal forma que nós, na Terra, recebemos pulsos de radiação dos pulsares em intervalos regulares iguais ao período de sua rotaç

Um próton sujeito a um campo magnético realiza um movimento helicoidal uniforme, com os seguintes parâmetros v x y = 5,00 x 10 5 m / s , a = 4,00 x 10 12 m / s 2 e v z = 2,00 x 10 4 m / s . Calcule o

As lâminas de um ventilador giram com velocidade angular dada por ω z t = γ - β t 2 , onde γ = 5r a d / s e β = 0,8r a d / s 3 . a) Calcule a aceleração angular em função do tempo. b) Calcule a aceler

Uma criança está empurrando um carrossel. O deslocamento angular do carrossel varia com o tempo de acordo com a relação θ t = γ t + β t 3 , onde γ = 0,4r a d / s e β = 0,012r a d / s 3 .a) Calcule a v

Uma roda gira em torno de um eixo que está na direção z . A velocidade angular ω z é - 6 rad/s para t = 0 , aumenta linearmente no decorrer do tempo e é + 8 rad/s para t = 7 s. Consideramos a rotação