UFSCAR, Sem Campus, Física 1, AV3 - 2021.2 - Prof° Raphael Santarelli, Questão 2b
Na figura abaixo dois blocos de mesma massa estão ligados por uma corda de massa desprezível, que passa por uma polia em formato de disco com raio e massa . A corda não escorrega na polia, e não há atrito no eixo da polia. Porém, existe atrito cinético entre a mesa e o bloco que escorrega. Quando o sistema é liberado a partir do repouso, a polia gira de em , e a aceleração dos blocos e da polia são constantes.
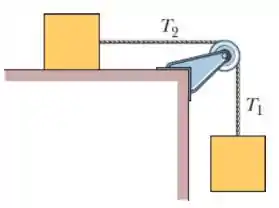
Qual a aceleração dos blocos?
Passo 1
E aí pessoal, tudo na paz?
Então, nessa questão temos dois blocos ligados por uma corda, que passa por uma polia. A grande diferença aqui é que essa polia não é ideal (de massa desprezível), mas ela possui massa . Enquanto os blocos possuem massa de Também é falado que o raio da polia vale .
O enunciado nos diz que o sistema é liberado do repouso e que em a polia girou . E, por fim, algo bem importante é que as acelerações do bloco e da polia são constantes.
Encontramos também, usando a equação horária para o movimento circular uniformemente variado, que a aceleração angular da polia vale:
A partir dessas informações precisamos determinar qual a aceleração dos blocos.
Então gente, a ideia principal aqui é utilizar o vínculo geométrico existente entre os dois lados do fio e também a aceleração linear dos pontos na extremidade da polia.
Vem comigo que vai ficar mais claro!
Passo 2
Bom, sabemos que a aceleração angular da polia é dada por:
Como a corda que une os blocos é inextensível precisamos que as acelerações com que a corda se movimenta em ambos os lados da polia sejam as mesmas. Mas, pelo vínculo geométrico, como as cordas estão presas aos blocos isso significa dizer que as acelerações dos blocos precisam ser iguais.
Seguindo o raciocínio, também pelo vínculo geométrico, o ponto da polia em contato com a corda em cada instante compartilha da mesma aceleração linear que a corda (já que a corda não escorrega na polia). E, consequentemente, que os blocos.
Assim, calcular a aceleração dos blocos resume-se a calcular a aceleração linear dos pontos na extremidade da polia!
Como , temos:
Excelente!!!
Conseguiram entender o raciocínio? Responde Aí!