Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Velocidade e Aceleração Médias no Movimento Circular

Ver Teoria
Exercício 6412345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626365

Enunciado

USP, Sem Campus, Física 1, Coletânea de Exercícios - Parte II - Colisões, Torque, Cinemática Angular, Questão 26c

Um disco uniforme de 100   k g e raio 0,60   m está sobre uma superfície de gelo lisa. Duas patinadoras gêmeas enrolam cordas em torno do disco, num mesmo sentido. Depois cada qual puxa a sua corda e se afasta do disco, exercendo sobre ele forças constantes F 1 → = ( 60   N ) i → e F → 2 = - ( 40   N )   i → durante 5   s .

( c ) Quantas voltas em torno de seu eixo o cilindro faz durante este tempo?

Passo 1

Oiie, tudo bem?

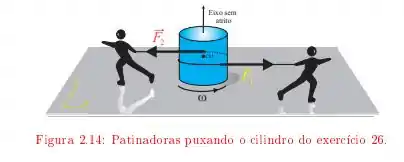
Temos aqui um disco uniforme que é puxado por duas patinadoras como no esquema a seguir

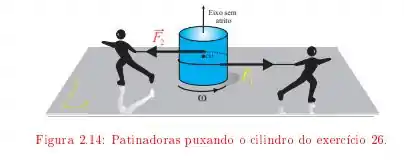
este disco tem uma massa m = 100   k g e raio r = 0,60   m . Elas aplicam forças F 1 → = ( 60   N )   i → e F → 2 = - ( 40   N )   i → de forma que o giro do disco é acelerado por ambas as forças durante 5   s , o objetivo desta alternativa é

( c ) Quantas voltas em torno de seu eixo o cilindro faz durante este tempo?

Na última alternativa obtivemos que

α → = 3,33   r a d   s - 2   k ^ e ω → ( t ) = ( 3,33   r a d   s - 2 )   t

usando estes dados podemos obter a expressão para a posição angular em termos do tempo! E, com isso em mãos ver a posição angular após t = 5   s , se uma volta são 2 π radianos, podemos estimar o número de voltas neste intervalo de tempo! Vamos lá!

Passo 2

Como a aceleração é constante, temos que a posição angular é dada pela equação horária para o movimento circular, obtemos que

θ ( t ) = 1 2 α → t 2 = ( 1,66   r a d   s - 2 )   t 2

Após t =   5 s nós obtemos que

θ = 41,6   r a d

se definirmos que o número de voltas é dado por

n = θ 2 π = 6,6   v o l t a s

Essa alternativa foi isso! Te vejo na próxima! Até já!

Resposta

n = 6,6   v o l t a s

Exercícios de Livros Relacionados

Pulsares são estrelas de nêutrons que emitem raios X e outras radiações de tal forma que nós, na Terra, recebemos pulsos de radiação dos pulsares em intervalos regulares iguais ao período de sua rotaç
Um próton sujeito a um campo magnético realiza um movimento helicoidal uniforme, com os seguintes parâmetros v x y = 5,00 x 10 5 m / s , a = 4,00 x 10 12 m / s 2 e v z = 2,00 x 10 4 m / s . Calcule o
As lâminas de um ventilador giram com velocidade angular dada por ω z t = γ - β t 2 , onde γ = 5r a d / s e β = 0,8r a d / s 3 . a) Calcule a aceleração angular em função do tempo. b) Calcule a aceler
Uma criança está empurrando um carrossel. O deslocamento angular do carrossel varia com o tempo de acordo com a relação θ t = γ t + β t 3 , onde γ = 0,4r a d / s e β = 0,012r a d / s 3 .a) Calcule a v
Uma roda gira em torno de um eixo que está na direção z . A velocidade angular ω z é - 6 rad/s para t = 0 , aumenta linearmente no decorrer do tempo e é + 8 rad/s para t = 7 s. Consideramos a rotação