Considere a figura abaixo que mostra uma conta que pode se
movimentar livremente, sem atrito, num aro circular de raio R 0,5 m
montado na vertical. O aro gira com velocidade angular constante de
módulo —14,9 rad/s em torno do seu eixo vertical. A conta está em
repouso em relação ao aro na posição indicada na figura, com 9 300.
Calcule a força centrípeta atuando sobre a conta.
Escolha uma:
a. 6,94 N
b. Nenhuma resposta está correta.
c. 8,33 N
d. 2,78 N
e. 5,55 N
f. 1,39 N
g. 4,16 N
h. 9,71 N
Passo 1
Opa galeeeeera! Hoje vamos relembrar sobre a sustentação de um yo-yo.
Vamos redesenhar o problema evidenciando as forças envolvidas:
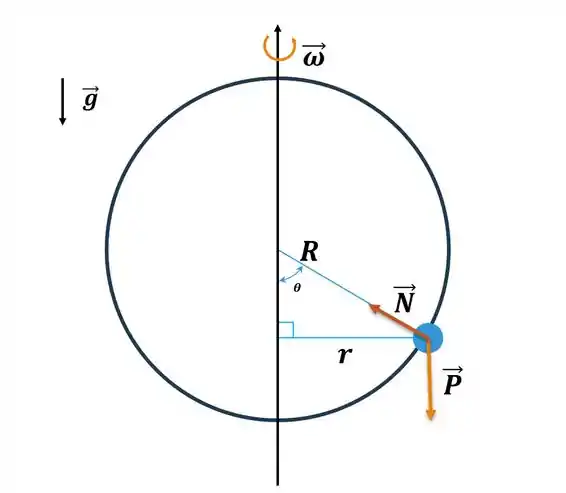
Note que:
– Raio do anel maior
– raio do anel menor
– Força normal que a superfície (anel maior) exerce no anel menor.
– Peso do anel menor
Passo 2
Sabendo que o anel menor terá a mesma velocidade angular que o maior por estarem rodando no mesmo eixo podemos utilizar a equação da força centrípeta:
E utilizando as relações trigonométricas do triangulo retângulo podemos estabelecer uma relação entre e :
Assim:
* Como a massa do anel menor não é dada, nem alguma outra informação que nos leve a ela, não é possível prosseguir com a conta. Todas as outras equações ficarão em função da massa e da força normal, sendo, portanto, um problema indeterminado.
Passo 3
Poderíamos utilizar o fato do anel não se mover na vertical para estabelecer uma relação entre a massa e a normal:
Passo 4
Poderíamos falar que a força centrípeta é a força horizontal resultante:
Resposta
Todas as respostas deste item no haviam sido dados como corretos pois com as informações providas nesta data não era possível determinar a força centrípeta numericamente.