Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Velocidade e Aceleração Médias no Movimento Circular

Ver Teoria
Exercício 1612345678910111213141517181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465

Enunciado

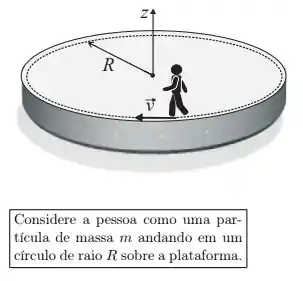
Uma pessoa de massa m está parada na borda de uma plataforma horizontal, de forma circular, com raio R e momento de inércia I que pode girar livremente em torno de um eixo vertical que passa pelo seu centro. Inicialmente, a plataforma está em repouso em relação ao solo. Num dado instante, a pessoa começa a andar ao longo da borda da plataforma, até atingir a velocidade de módulo v em relação ao solo, como mostra a figura. Neste instante, a velocidade angular da plataforma vale:

  1. Zero.
  2. ω → = - m R 2 / I ( v / R )   k →  
  3. ω → = + m R 2 / I ( v / R )   k →
  4. ω → = - ( v / R )   k →
  5. ω → = + ( v / R )   k →

Passo 1

“AH! Tranquilo essa! afinal v = ω R então ω → = v / R   k → ”

Diga-me aí: por que esse raciocínio de cima está errado para este problema?

Ora! Se estivéssemos falando apenas do disco girando com velocidade v → , de fato poderíamos utilizar v = ω R . Mas não é bem isso que está acontecendo.

O que está acontecendo é uma pessoa que tem massa m em cima do disco e que está andando a uma velocidade v → . Só o fato de ter um ponto com massa m ali em cima já muda o momento de inércia total do disco e, portanto, muda também a velocidade angular desse disco.

“Ta, então como que a gente encontra isso?”

Bem, a dica está dada ali em cima: se o momento de inércia total do sistema muda. Vamos calcular ω através da sua relação com o momento de inércia, ou seja, pela fórmula L → = I s i s ω → , onde L → é o momento angular e I s i s é o momento de inércia do sistema Pessoa + disco.

Passo 2

Cara! Então... Temos aqui um sistema formado por duas coisas girando: uma partícula (a pessoa) e o disco. Então, o momento angular total vai ser o momento dessas duas coisas:

L → t o t = L → p a r t + L → d i s c

Só que o sistema (disco+pessoa) não tem nenhuma ação de força externa atuando. Logo, podemos concluir que o momento angular total tem que ser igual a 0 :

L → p a r t + L → d i s c = 0

O momento angular da partícula é igual a I p a r t ω p a r t e o do disco vai ser I ω ...

I p a r t ω p a r t → + I ω → = 0

Agora sim! Olha que interessante! A velocidade angular da partícula ω p a r t → pode ser visto como v / R , afinal v é a velocidade do carinha e R é o raio que a partícula está girando. O momento de inércia de partícula é m R 2 ...

m R 2 v R - k → + I ω → = 0

O - k → serve para dar a direção e o sentido da velocidade angular ω p a r t → . Pela regra da mão direita em cima do carinha andando teremos que o sentido da velocidade angular dele de fato vai ser para baixo (na direção z ) daí o - k → .

Então, a velocidade angular do disco e agora levando em consideração o ser humano no disco...

ω → = m R 2 I v R k →

Resposta

Letra C.

Exercícios de Livros Relacionados

Pulsares são estrelas de nêutrons que emitem raios X e outras radiações de tal forma que nós, na Terra, recebemos pulsos de radiação dos pulsares em intervalos regulares iguais ao período de sua rotaç
Um próton sujeito a um campo magnético realiza um movimento helicoidal uniforme, com os seguintes parâmetros v x y = 5,00 x 10 5 m / s , a = 4,00 x 10 12 m / s 2 e v z = 2,00 x 10 4 m / s . Calcule o
As lâminas de um ventilador giram com velocidade angular dada por ω z t = γ - β t 2 , onde γ = 5r a d / s e β = 0,8r a d / s 3 . a) Calcule a aceleração angular em função do tempo. b) Calcule a aceler
Uma criança está empurrando um carrossel. O deslocamento angular do carrossel varia com o tempo de acordo com a relação θ t = γ t + β t 3 , onde γ = 0,4r a d / s e β = 0,012r a d / s 3 .a) Calcule a v
Uma roda gira em torno de um eixo que está na direção z . A velocidade angular ω z é - 6 rad/s para t = 0 , aumenta linearmente no decorrer do tempo e é + 8 rad/s para t = 7 s. Consideramos a rotação