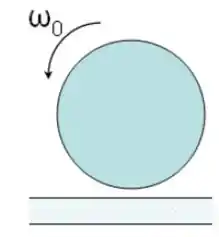
Uma esfera uniforme de raio e massa gira com velocidade angular inicial em torno do eixo horizontal que passa pelo seu centro, conforme figura ao lado (eixo saindo do papel). Ela é então colocada, no instante , suavemente sobre um piso, cujo coeficiente de atrito cinético com a bola é . Note que no instante inicial em que ela é colocada no piso, ela só possui rotação sem translação (ela está inicialmente só patinando).

Determine o tempo necessário para ela deixar de patinar, e começar a rolar sem deslizar (rolamento suave).

Quando ela atinge a condição de rolamento suave, qual é a velocidade linear do seu centro de massa e sua velocidade angular de rotação em torno do centro de massa?

Qual a energia térmica produzida entre o instante inicial e o instante em que atinge o rolamento suave?

Pra começar, precisamos determinar em quanto tempo a esfera deixa de patinar.

Então galera, como comentamos no passo anterior, a esfera só para de patinar quando a velocidade do ponto de contato da esfera com a superfície se torna nulo.

Como nesse ponto de contato só age a força de atrito, podemos dizer pela Lei de Newton que:

Como na vertical a esfera está em equilíbrio, e só age a força normal e a força peso, temos:

Logo, a força de atrito cinético, vale:

Logo, temos:

Beleza! Essa força é contrária à velocidade do ponto de contato. Como ela é a única componente horizontal, dizemos que ela está acelerando o centro de massa da esfera, lhe concedendo velocidade linear.

Assim, podemos escrever a velocidade da esfera quando inicia o rolamento suave como:

Mas, como comentamos, a força de atrito também está produzindo um torque que desacelera a velocidade angular de rotação da esfera segundo a equação:

O torque da força de atrito é dado por:

Já o momento de inércia com relação ao centro da esfera é dado por:

Logo:

Logo, sobre a velocidade angular da esfera podemos afirmar quando inicia o rolamento suave, ela vale:

Assim, como o ponto de contato vai estar “parado” quando inicia o rolamento, podemos usá-lo como centro instantâneo de rotação. Dessa forma, a velocidade do centro de massa da esfera pode ser escrito como:

Igualando as duas equações que encontramos para a velocidade do centro de massa, temos que:

Logo:

Muito bom! A primeira parte foi!

Como já temos o tempo podemos descobrir a velocidade angular de rotação da esfera quando inicia o rolamento pela equação que desenvolvemos no passo anterior:

Substituindo o valor de , temos:

Portanto:

Muito bom!

Pra calcular a velocidade linear podemos usar o mesmo raciocínio.

Vimos que:

Substituindo , temos:

(que já era esperado pelo resultado de .

Tudo tranquilo até aqui? Vamos pro último itemmm!!

Aqui precisamos calcular a energia térmica dissipada entre o instante inicial e o instante em que inicia o rolamento.

A ideia é usarmos que a variação de energia mecânica do sistema é igual à energia térmica dissipada.

Assim, vamos começar calculando a energia mecânica do sistema em .

Como havia apenas rotação da esfera, temos que:

Logo:

Então:

Já quando inicia o rolamento suave, temos tanto movimento de rotação como de translação. Daí:

Substituindo os valores que calculamos para e no item anterior, vem:

Logo:

Daí, usando que:

Vem que:

Logo:

onde o sinal negativo indica apenas que essa energia foi dissipada.