James Stewart, Cálculo Vol. 2, 7ª ed. Capítulo 11. Seção 2. Questão 7.
(Cap. 11.2 – Ex. 7) Calcule os oito primeiros termos da sequência de somas parciais corretas para quatro casas decimais. Parece que a série é convergente ou divergente?
Passo 1
Iae, meus queridos! Tudo certinho?
Então galera, essa questão quer que testemos nosso conceito sobre séries. Como assim? Uma série é dita divergente ou convergente se, e somente se, a sequência de somas parciais também for divergente ou convergente, respectivamente. A sequência que nos foi dada é essa aqui
Agora vamos ter que calcular os oito primeiros termos da sequência de somas parciais.
Para :
Para , teríamos:
Repara que é sempre a soma com o termo anterior, seguindo teríamos:
Passo 2
Vamos substituir por para calcular , por para calcular a e assim por diante
Calculando os termos da sequência
Para , temos
Para , temos
Para , temos
Para , temos
Para , temos
Para , temos
Para , temos
Por fim, para , temos
Podemos notar que a sequência não está tendendo para um valor específico, não é mesmo? A cada termo que calculamos o valor da sequência muda. Sendo assim, a conclusão é de que a série está divergindo, ou seja, não está tendendo para um valor específico. Em outras palavras, a série divergente.
Graficamente vemos que a os pontos se distanciam muito lentamente de uma reta tangente à curva que liga os dois primeiros pontos
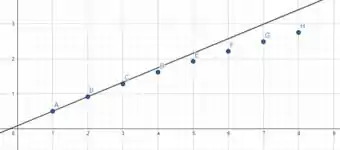
Isso é outro indício que a série diverge.
Iae, entendeu tudo? Responde Aí 😎👍
Bora praticar mais!