James Stewart, Cálculo Vol. 2, 7ª ed. Capítulo 11. Seção 2. Questão 8.
(Cap. 11.2 – Ex. 8) Calcule os oito primeiros termos da sequência de somas parciais corretas para quatro casas decimais. Parece que a série é convergente ou divergente?
Passo 1
Iae, meus queridos! Tudo certinho? 👍
Então galera, essa questão quer que testemos nosso conceito sobre séries. Como assim? Uma série é dita divergente ou convergente se, e somente se, a sequência de somas parciais também for divergente ou convergente, respectivamente. A sequência que nos foi dada é:
Para calcularmos os oito primeiros termos da sequência de somas parciais, teremos que fazer:
Se notarmos que a sequência está tendendo para um valor fixo, então a conclusão será de que a mesma é convergente. Caso contrário, então a conclusão será de que a mesma é divergente. Sem mais delongas, mãos à obra!
Passo 2
Vamos substituir por para calcular , por para calcular a e assim por diante
Calculando os termos da sequência
Para , temos
Para , temos
Para , temos
Para , temos
Para , temos
Para , temos
Para , temos
Para , temos
Podemos notar que a sequência tende para um valor em torno de . Sendo assim, a conclusão é de que a série é convergente e converge para .
Graficamente, vemos que quanto maior o , a soma se aproxima de
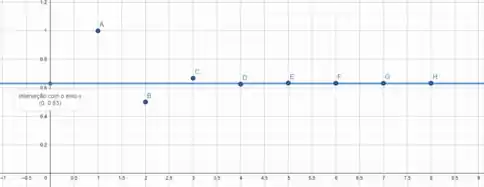
É isso! Entendeu tudo? Responde Aí 😎👍