Cálculo - James Stewart - Volume 2 - 7ª Edição – Capítulo 11 – Seção 10 – Exercício 2
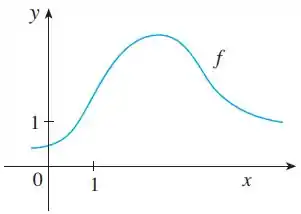
(Capítulo 11.10 – Exercício 2) O gráfico de é mostrado.
(a) Explique por que a série
não é a série de Taylor de centrada em .
(b) Explique por que a série
não é a série de Taylor de centrada em .
Passo 1
Falaaa galera, vamos falar sobre série de Taylor
Nessa questão, temos o gráfico de uma função , dado assim:
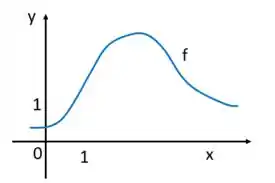
E aí queremos analisar esse gráfico com foco na série de Taylor
Só relembrando aqui, a série de Taylor é escrita assim:
Onde é a enésima derivada no ponto , e o ponto é o ponto central da nossa série
Ou seja, isso vai gerar uma soma do tipo:
Agora vamos lá analisar o nosso problema
Passo 2
a) Aqui vamos explicar porque
Não pode ser a série de Taylor da função centrada em
No ponto podemos observar no gráfico que a função está crescente, portanto sua primeira derivada deve ser positiva
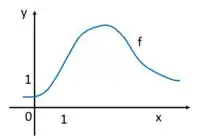
Porém, na Série de Taylor, o coeficiente que acompanha uma potência de , carrega o sinal da enésima derivada, já que no formato de Taylor o fatorial é sempre positivo, certo?
Ou seja: é a derivada quem decide o sinal do termo
Se olharmos para a série que foi dada, no segundo termo , temos um termo negativo, o que implica na primeira derivada negativa, o que não condiz com a função do gráfico, fechou?
Passo 3
(b) Agora vamos analisar a série
A primeira derivada aqui está com sinal positivo, pois o primeiro termo é
Show! Isso condiz com a função estar crescente em , não temos o mesmo problema da letra A
Porém, o 2° termo é
, em que temos um sinal positivo
Uma 2ª derivada positiva representa uma concavidade para cima, certo?
Mas no gráfico podemos observar que temos uma concavidade para baixo em
Logo, a série não condiz com a função do gráfico.
Resposta
Ei, a resposta está no passo a passo :)