Exercícios Resolvidos de Projeção Ortogonal

Exercício 40 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 41 42 43 44 45 46 47

Enunciado

UFRJ, P3-2019.1

Assinale a distância do vetor á sua reflexão ortogonal pelo plano de equação :

Passo 1

Chuchu beleza galerinha bonita, queremos encontrar a distância do vetor á sua reflexão ortogonal pelo plano de equação :

Mas calma aí meu chefe, porque esse exercício é sagacidade pura. Saca só, vamos imaginar que a gente olhando pro nosso plano meio que “de lado”, e o nosso vetor em cima dele, mais ou menos assim:

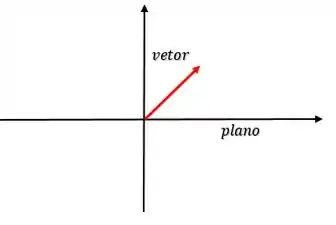
Se a gente refletisse o vetor ortogonalmente, teríamos:

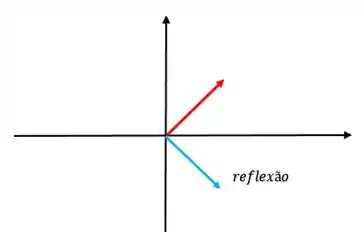
Portanto, a distância entre o vetor e a sua reflexão é:

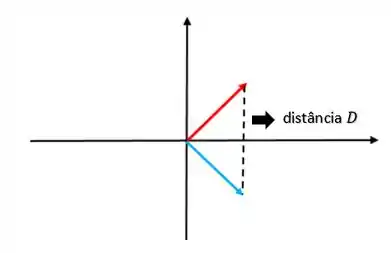
Passo 2

Mas agora que começa a malandragem porque a gente não precisa calcular a reflexão e depois calcular a distância. Porque saca só, essa distância pode ser dividida em duas:

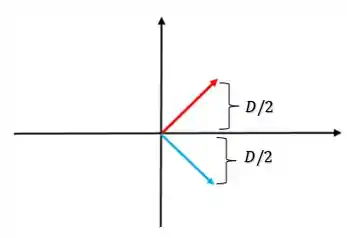
Só que essa metade da distância, é exatamente igual a Projeção Ortogonal do vetor no complemento ortogonal do plano.

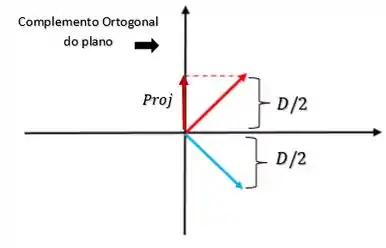
Então quer dizer que a distância , pode ser expressa como:

Passo 3

Agora ficou bonitinho, o complemento ortogonal da plano , é exatamente os coeficientes que acompanham as varáveis:

Logo o complemento ortogonal é . Xuxu beleza, então a projeção de em é dada por:

Logo, a distância é:

Portanto o módulo de é:

Resposta certa, letra (b)

Resposta

Letra (b).

Exercícios de Livros Relacionados

Seja A uma matriz m × n com vetores coluna linearmente independentes. Obtenha a matriz canônica da projeção ortogonal de R n no espaço coluna de A . [Sugestão: comece com a Fórmula 10 .]

Seja W a reta de equações paramétricas x = 2 t , y = - t , z = 4 t Encontre uma base de W .Use a Fórmula 10 para encontrar a matriz canônica da projeção ortogonal em W .Use a matriz obtida na parte b

Seja W o plano de equação 5 x - 3 y + z = 0 .Encontre uma base de W .Use a Fórmula 10 para encontrar a matriz canônica da projeção ortogonal em W .Use a matriz obtida na parte b para encontrar a proje

Em cada parte, encontre det ⁡ A T A e aplique o Teorema 6.4 . 3 para determinar se A tem vetores coluna linearmente independentes. A = - 1 3 2 2 1 3 0 1 1

Use a Fórmula (10) e o método do Exemplo 3 para encontrar matriz canônica da projeção ortogonal P : R 2 → R 2 No eixo x .[Observação: compare suas respostas com a Tabela 4 da Seção 4.9.]