Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Projeção Ortogonal

Ver Teoria
Exercício 3312345678910111213141516171819202122232425262728293031323435363738394041424344454647

Enunciado

USP, PSUB, 2019, Q9

Em E 3 , sejam π 1   e   π 2 planos cujas interseção é uma reta r. Sejam n 1 →   e n 2 → vetores não-nulos de V 3 tais que n 1 → ⊥ π 1 e n 2 → ⊥ π 2 , e seja v → ∈ V 3 um vetor não-nulo paralelo a r. Considere as seguintes afirmações:

I .   O s   v e t o r e s   v →   e   n 1 → ∧ n 2 → são paralelos

I I .   B = n 1 →   ,   n 2 → , v → é uma base ortogonal de V 3

I I I .   O   c o n j u n t o   v → , v →   ∧   n 1 → ,   v →   ∧   n 2 →   é linearmente independente

Está correto o que se afirma em

a )     I   e   I I ,   a p e n a s

b )   I , I I   e   I I I

c )   I   e   I I I ,   a p e n a s

d )   I I ,   a p e n a s

e )   I I I ,   a p e n a s

Passo 1

Faaaaalaaaa, tranquilo???? Bora começar essa questão dando uma visualizada no que está ocorrendo na questão

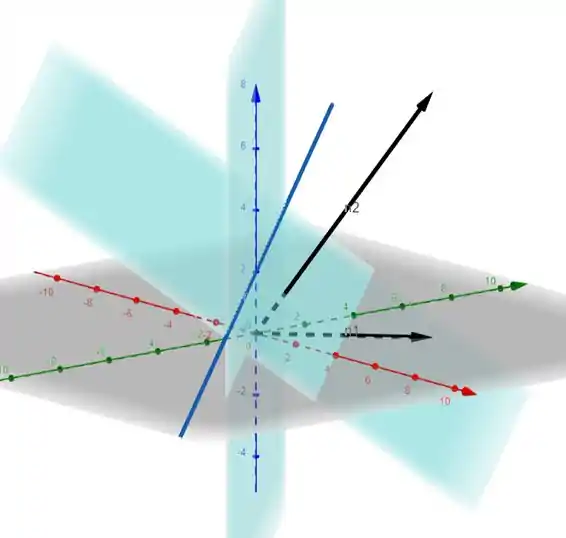
Passo 2

Agora tendo essa imagem para nos ajudar, bora checar as alternativas.

I .   O s   v e t o r e s   v →   e   n 1 → ∧ n 2 → são paralelos

Para analisar essa afirmação, vale lembrar que o resultado de n 1 → ∧ n 2 → é um vetor perpendicular, ao mesmo tempo, a n 1 →   e n 2 → . Porém, veja que n 1 →   e n 2 → são perpendiculares ao plano π 1   e   π 2 , ou seja, um vetor perpendicular a n 1 → será um vetor paralelo ao plano, o mesmo vale para um vetor perpendicular a n 2 → . Ou seja n 1 → ∧ n 2 → é paralelo aos planos π 1   e   π 2 ao mesmo tempo, isso te faz lembrar algo?

Nosso vetor v → está sobre uma reta que é interseção de π 1   e   π 2 , ou seja, é paralelo aos 2. Portanto, podemos dizer que   v →   e   n 1 → ∧ n 2 → são paralelos

Bora para a próxima afirmação.

I I .   B = n 1 →   ,   n 2 → , v → é uma base ortogonal de V 3

Essa afirmação é falsa, basta olharmos na nossa figura, por exemplo, e verá que n 1 →   ,   n 2 → não são ortogonais.

Passo 3

Agora falta ver a última afirmação.

I I I .   O   c o n j u n t o   v → , v →   ∧   n 1 → ,   v →   ∧   n 2 →   é linearmente independente

Essa afirmação é verdadeira, pois v →   ∧   n 1 → é perpendicular a v → e v →   ∧   n 2 → também, além disso v →   ∧   n 1 → ,   v →   ∧   n 2 → são não paralelos, pela hipótese de v não ser nulo. Pois se v →   ∧   n 1 → ,   v →   ∧   n 2 → fossem paralelos, teríamos que os planos seriam paralelos, quebrando a hipótese de v (ou a interseção seria um plano, não uma reta, ou não haveria interseção e v seria nulo)

Logo os três são L.I

Resposta

Letra C

Exercícios de Livros Relacionados

Seja A uma matriz m × n com vetores coluna linearmente independentes. Obtenha a matriz canônica da projeção ortogonal de R n no espaço coluna de A . [Sugestão: comece com a Fórmula 10 .]
Seja W a reta de equações paramétricas x = 2 t , y = - t , z = 4 t Encontre uma base de W .Use a Fórmula 10 para encontrar a matriz canônica da projeção ortogonal em W .Use a matriz obtida na parte b
Seja W o plano de equação 5 x - 3 y + z = 0 .Encontre uma base de W .Use a Fórmula 10 para encontrar a matriz canônica da projeção ortogonal em W .Use a matriz obtida na parte b para encontrar a proje
Em cada parte, encontre det ⁡ A T A e aplique o Teorema 6.4 . 3 para determinar se A tem vetores coluna linearmente independentes. A = - 1 3 2 2 1 3 0 1 1
Use a Fórmula (10) e o método do Exemplo 3 para encontrar matriz canônica da projeção ortogonal P : R 2 → R 2 No eixo x .[Observação: compare suas respostas com a Tabela 4 da Seção 4.9.]