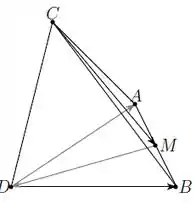
Considere um tetraedro tal que, em alguma base ortonormal , , é um ponto da aresta , e .
a) Calcule o volume do tetraedro .
b) Determine o vetor .
c) Mostre que é uma base ortonormal.
Passo 1
a) O volume do tetraedro vai ser dado por do produto misto de , e , ou seja:
Mas peraí, não temos o vetor , então vamos encontrar:
Passo 2
Belezinha, agora podemos fazer aquele produto misto:
Agora, sabendo que , temos que
Passo 3
b) vai ser a projeção de em , ou seja:
Passo 4
c) Os vetores que temos aqui são:
Para que esses 3 vetores formem uma base ortonormal, todos eles devem ter módulo e devem ter entre si, ou seja, o produto interno de um com o outro deve sempre ser .
Primeiro vamos encontrar o módulo de cada um:
Boa!! Já provamos que todos eles têm módulo 1! Agora vamos fazer o produto interno entre eles dois a dois pra provarmos que sempre vai dar 0!!
Passo 5
Fazendo os produtos internos:
Legal!! Todos os produtos internos deram 0!!
Ta provado que todos esses vetores têm norma 1 e são ortogonais entre si, então, de fato, formam uma base ortonormal!!
Resposta
a)
b)
c) Demonstração.