Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Projeção Ortogonal

Ver Teoria
Exercício 3512345678910111213141516171819202122232425262728293031323334363738394041424344454647

Enunciado

USP, P2, 2017, 3

Considere o vetor z → = 1,1 , 1 , o plano

π : x - 2 y + 3 z - 6 = 0

E sejam v → ,   w →   ∈ V 3 tais que z → = v → + w → , em que v → é ortogonal a π e w → é paralelo a π . Se w → = ( a , b , c ) , então a + b + c será igual a:

a   2

b 15 7

c   3

d 19 7

e 16 7

Passo 1

Falaaaa, blz?? Bora começar essa questão fazendo um desenho para entendermos o que podemos fazer:

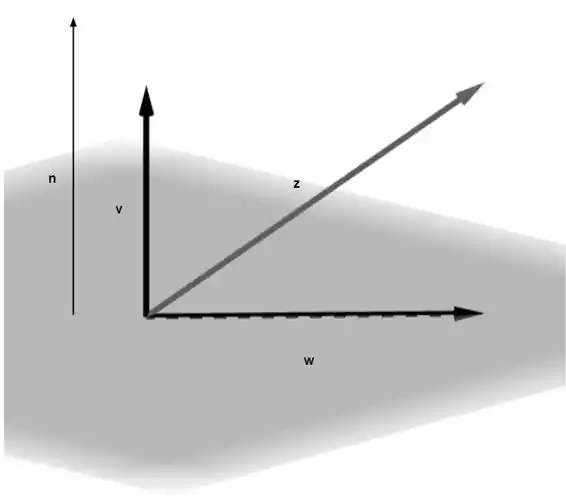
Na figura, temos que n → = 1 , - 2,3 ⊥ π

Nosso objetivo na questão é achar w → , e temos z → = v → + w → , ou seja z → - v → = w →

Para achar w → basta achar v → , pois já temos z → , bora fazer isso?

Passo 2

Bora buscar agora uma forma de achar v →

Olhando para figura, fica mais intuitivo o que está ocorrendo, veja que temos a seguinte igualdade:

v → = P r o j n → ( z → )

E temos uma fórmula para calcular essa projeção, bora fazer isso?

v → = z → , n → n → 2 n → = 1 - 2 + 3 14 n → = 2 14 n → = 1 7 n → = 1 7 , - 2 7 , 3 7

Passo 3

Agora é só finalizar o problema, bora lá:

w → = z → - v → = 1,1 , 1 - 1 7 , - 2 7 , 3 7 = 6 7 , 9 7 , 4 7

Ou seja, a nossa resposta é 6 7 + 9 7 + 4 7 = 19 7 , fazendo a gente chegar numa resposta, probleminha um pouco chato, que força a gente enxergar algumas coisa, porém deu tudo certo, bora para o próximo?

Resposta

Letra D

Exercícios de Livros Relacionados

Seja A uma matriz m × n com vetores coluna linearmente independentes. Obtenha a matriz canônica da projeção ortogonal de R n no espaço coluna de A . [Sugestão: comece com a Fórmula 10 .]
Seja W a reta de equações paramétricas x = 2 t , y = - t , z = 4 t Encontre uma base de W .Use a Fórmula 10 para encontrar a matriz canônica da projeção ortogonal em W .Use a matriz obtida na parte b
Seja W o plano de equação 5 x - 3 y + z = 0 .Encontre uma base de W .Use a Fórmula 10 para encontrar a matriz canônica da projeção ortogonal em W .Use a matriz obtida na parte b para encontrar a proje
Em cada parte, encontre det ⁡ A T A e aplique o Teorema 6.4 . 3 para determinar se A tem vetores coluna linearmente independentes. A = - 1 3 2 2 1 3 0 1 1
Use a Fórmula (10) e o método do Exemplo 3 para encontrar matriz canônica da projeção ortogonal P : R 2 → R 2 No eixo x .[Observação: compare suas respostas com a Tabela 4 da Seção 4.9.]