Se é um pentágono regular de lado como na figura abaixo, determine
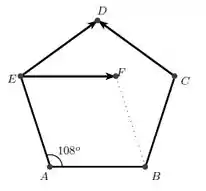
a) . (Dado: )
b) O valor de para o qual
Passo 1
a) O vetor é equivalente ao vetor , só que agora com origem em .
O triângulo é isósceles, então usando as regrinhas lá de trigonometria, sabemos que o ângulo entre e é .
Então agora vamos só aplicar a formulazinha de produto escalar:
Passo 2
b) O ângulo entre e é o suplementar de , ou seja, (o seu cosseno vai ser o oposto do cosseno de )
Então vamos calcular a projeção de em :
Então o que multiplica o vetor no resultado da projeção é .
Resposta
a)
b)
Exercícios de Livros Relacionados
Seja A uma matriz m × n com vetores coluna linearmente independentes. Obtenha a matriz canônica da projeção ortogonal de R n no espaço coluna de A . [Sugestão: comece com a Fórmula 10 .]
Seja W a reta de equações paramétricas x = 2 t , y = - t , z = 4 t Encontre uma base de W .Use a Fórmula 10 para encontrar a matriz canônica da projeção ortogonal em W .Use a matriz obtida na parte b
Seja W o plano de equação 5 x - 3 y + z = 0 .Encontre uma base de W .Use a Fórmula 10 para encontrar a matriz canônica da projeção ortogonal em W .Use a matriz obtida na parte b para encontrar a proje
Em cada parte, encontre det A T A e aplique o Teorema 6.4 . 3 para determinar se A tem vetores coluna linearmente independentes. A = - 1 3 2 2 1 3 0 1 1
Use a Fórmula (10) e o método do Exemplo 3 para encontrar matriz canônica da projeção ortogonal P : R 2 → R 2 No eixo x .[Observação: compare suas respostas com a Tabela 4 da Seção 4.9.]