Considere o ponto e o plano . Determine
a) A projeção ortogonal de sobre .
b) O ponto simétrico de em relação a .
Passo 1
a) A projeção ortogonal de no plano vai ser um ponto que é a intersecção do plano com uma reta perpendicular a ele que passe pelo ponto .
Para que essa reta seja perpendicular a , seu vetor diretor deve ser um vetor normal do plano certo? Logo:
Passo 2
Beleza, agora que temos a reta vamos encontrar . Um ponto genérico de é , vamos substituir esse ponto na equação do plano:
Substituindo no ponto , vamos ter
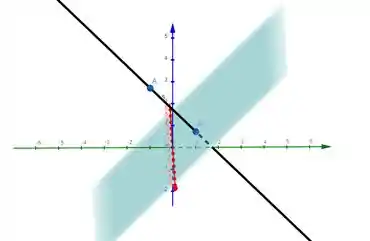
Abaixo vemos em azul claro o plano , em preto a reta e em azul escuro os pontos e .
Passo 3
b) O ponto simétrico de em relação a vai ser o ponto tal que
Por propriedades de vetores, isso nos dá
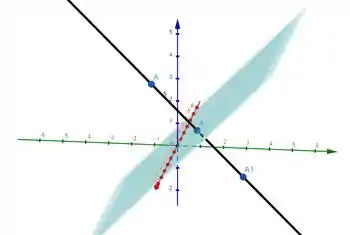
Abaixo temos a inclusão do ponto , que podemos reparar que é, de fato, simétrico a em relação ao plano.
Resposta
a)
b)