Dados os planos e , a reta e o ponto :

Sabendo que é um tetraedro e que a face tem lado com medida é um triângulo retângulo em e está contido em , a face está contida em e o vértice , determine as coordenadas dos pontos , e .

(Obs: o ponto já é conhecido).

Beleza, já achamos o ponto . Agora vamos mexer com e ok?

Do enunciado, a gente sabe que a aresta está contida tanto no plano como em . Então essa aresta pertence à reta fechou?

Antes de encontrar a reta , vamos encontrar a equação geral de :

Então, a equação geral de é

Beleza, agora vamos encontrar a reta , que é a intersecção dos planos:

Subtraindo as duas equações, temos:

Substituindo isso na primeira equação:

Logo, tendo como nosso parâmetro , podemos escrever a equação paramétrica da reta :

Então um ponto da reta é e seu vetor diretor é .

Olha o que a gente já tem por enquanto:

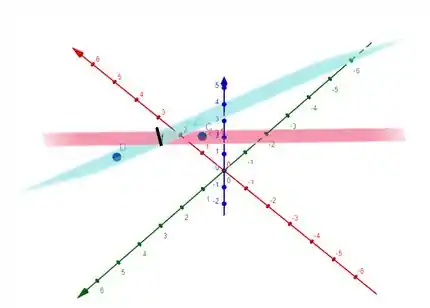
O plano rosa é e o plano azul é . A reta preta é .

Como a gente já concluiu lá no passo 2, a aresta vai estar na reta certo?

Mas agora vamos lembrar de outra informação do enunciado: a face é um triângulo retângulo em , ou seja, .

Portaaanto, o ponto vai ser a projeção ortogonal de na reta , enquanto o ponto vai estar em algum lugar ao longo dessa reta.

Pra encontrarmos a projeção de em vamos fazer a projeção do vetor no vetor diretor de , o que encontramos no passo 3. Isso vai dar pra gente o vetor , e aí a gente encontra :)

Ta aqui um esbocinho em outro ângulo e sem o plano pra gente enxergar o que ta acontecendo. O vetor verde é , e a projeção ortogonal dele ali no vetor diretor da reta , vai ser o vetor (o ponto é o vinho e o ponto é o roxo).

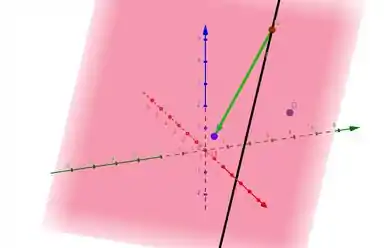
Então bora fazer a projeção ortogonal de em :D

Sabendo que :

Sabendo que :

Aeee, agora só falta acharmos o vértice .

Como a aresta está na reta , é paralelo a , o vetor diretor de , então:

Onde é algum número escalar.

Aplicando módulo dos dois lados da igualdade (lembrando que )

Se

Se

Boaaa, achamos todos os nossos vértices :D