Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Projeção Ortogonal

Ver Teoria
Exercício 4412345678910111213141516171819202122232425262728293031323334353637383940414243454647

Enunciado

UFRJ, P4-2019.2

Que múltiplo do vetor u → = 1 ,   3 ,   5 ,   2 está o mais próximo possível do vetor v → = 1 ,   1 ,   4 ,   3 ?

  1. 10 13 u → .
  2. 32 39 u → .
  3. 28 39 u → .
  4. 9 13 u → .

Passo 1

Belezoca galerinha, esse exercício é pura malandragem, saca só, a gente quer encontrar um vetor w → múltiplo de u → = 1 ,   3 ,   5 ,   2 que esteja o mais próximo possível de v → = 1 ,   1 ,   4 ,   3 . Como o vetor w → é múltiplo de u → , quer dizer que ele pertence a reta gerada por u → .

O vetor v → está fora do vetor u → , tal que:

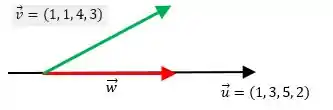
Portanto, a menor distância entre o múltiplo w → e o vetor v → é dada como:

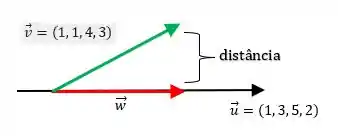
E o bizu master que a gente pode ter aqui é que o múltiplo w → que tem a menor distância com o vetor v → é exatamente a projeção ortogonal do vetor v → no vetor u → :

w → = P r o j u → v →

Passo 2

Iradoso, agora que já temos o segredo do universo em nossas mãos, podemos calcular de fato esse vetor w → . A fórmula da projeção ortogonal de um vetor v → sobre um vetor u → é dada por:

P r o j u → v → = v → ,   u → u → ,   u → u →

Logo, para nossos vetores u → = 1 ,   3 ,   5 ,   2 e v → = 1 ,   1 ,   4 ,   3 , temos que:

P r o j u → v → = 1 ,   1 ,   4 ,   3 ,   1 ,   3 ,   5 ,   2 1 ,   3 ,   5 ,   2 ,   1 ,   3 ,   5 ,   2 u →

Resolvendo então os produtos internos, obtemos:

P r o j u → v → = 1 1 + 1 3 + 4 5 + 3 ( 2 ) 1 2 + 3 2 + 5 2 + 2 ² u →

P r o j u → v → = 1 + 3 + 20 + 6 1 + 9 + 25 + 4 u →

P r o j u → v → = 30 39 u →

P r o j u → v → = 10 13 u →

Portanto, o vetor w → múltiplo de u → e mais próximo de v → é dado por:

w → = 10 13 u →

Resposta certa, letra (a)

Resposta

Letra (a).

Exercícios de Livros Relacionados

Seja A uma matriz m × n com vetores coluna linearmente independentes. Obtenha a matriz canônica da projeção ortogonal de R n no espaço coluna de A . [Sugestão: comece com a Fórmula 10 .]
Seja W a reta de equações paramétricas x = 2 t , y = - t , z = 4 t Encontre uma base de W .Use a Fórmula 10 para encontrar a matriz canônica da projeção ortogonal em W .Use a matriz obtida na parte b
Seja W o plano de equação 5 x - 3 y + z = 0 .Encontre uma base de W .Use a Fórmula 10 para encontrar a matriz canônica da projeção ortogonal em W .Use a matriz obtida na parte b para encontrar a proje
Em cada parte, encontre det ⁡ A T A e aplique o Teorema 6.4 . 3 para determinar se A tem vetores coluna linearmente independentes. A = - 1 3 2 2 1 3 0 1 1
Use a Fórmula (10) e o método do Exemplo 3 para encontrar matriz canônica da projeção ortogonal P : R 2 → R 2 No eixo x .[Observação: compare suas respostas com a Tabela 4 da Seção 4.9.]