Considere o produto interno usual de e calcule a distância entre o ponto e a reta gerada pelo vetor
- .
- .
- .
- .
Passo 1
Show de belezeras galerinha, queremos calcular a distância entre o ponto e a reta gerada pelo vetor , ambos do .

Vamos devagarinho pessoal, como estamos em a parte visual fica um pouco comprometida. Mas a gente pode extrapolar um pouquinho e imaginar que o ponto e a reta no espaço são:
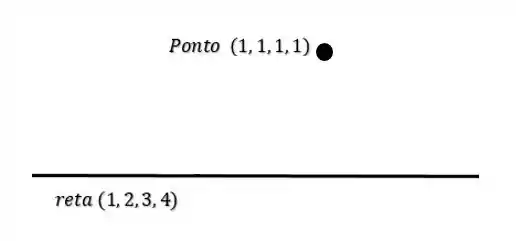
Portanto, a distância entre eles é:
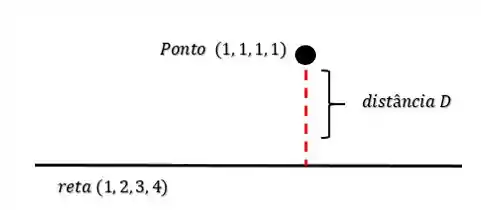
Isso quer dizer que se por um acaso tivéssemos um ponto tal que:
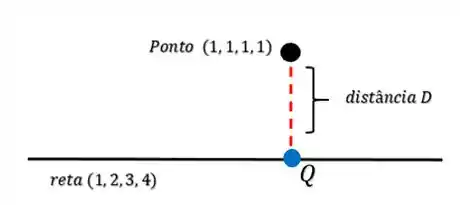
Então poderíamos dizer que a distância é:
Passo 2
MAAASSS é aí que tá a malandragem, porque esse ponto é exatamente a projeção ortogonal de sobre a reta . Então encontrar é a mesma coisa que encontrar essa projeção ortogonal:
E pra calcularmos a projeção de um ponto em uma reta , temos a fórmula:
Então passando para os nossos dados, temos que:
Então isso quer dizer que nosso ponto é:

Passo 3
Xuxu beleza então, como vimos no Passo 1, a distância é medida pela relação:
E o ponto que encontramos é , logo:
O módulo dessa distância é:

Calma lá galerinha, não tem essa resposta no enunciado, mas nada de pânico. Podemos fazer algumas mudancinhas na nossa resposta afim de encontrar alguma coisa legal. Saca só, podemos abrir a raiz quadrada do numerador, desse jeito:
E podemos abrir o denominador, desse jeito:
E num passe de mágica, cortamos as raízes e ficamos assim:
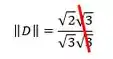
Agoooora sim. Então quer dizer que nossa reposta é a alternativa (c).

Resposta
Letra (c).