USP, 2018.1, P2, Q7
Considere o vetor e o plano . Se com //, , então é igual a:
Passo 1
Falaaaa, beleza??? Bom, nessa questão a motivação aparece quando desenhamos o que tá rolando, então vamos fazer isso:
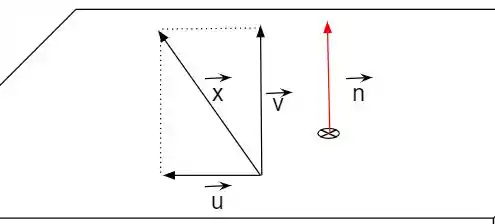
Veja que pela figura nós temos a seguinte situação:
é a projeção do vetor na direção do vetor normalao plano
Lembrando que se temos um plano do tipo o vetor é um vetor normal ao plano.
No nosso plano temos que é normal a .
Passo 2
Vamos lembrar a “fórmula” para calcular a projeção de um vetor sobre outro...
A projeção de sobre é dada por:
Passo 3
Vamos substituir os valores da questão:
Logo
Resposta
Exercícios de Livros Relacionados
Seja A uma matriz m × n com vetores coluna linearmente independentes. Obtenha a matriz canônica da projeção ortogonal de R n no espaço coluna de A . [Sugestão: comece com a Fórmula 10 .]
Seja W a reta de equações paramétricas x = 2 t , y = - t , z = 4 t Encontre uma base de W .Use a Fórmula 10 para encontrar a matriz canônica da projeção ortogonal em W .Use a matriz obtida na parte b
Seja W o plano de equação 5 x - 3 y + z = 0 .Encontre uma base de W .Use a Fórmula 10 para encontrar a matriz canônica da projeção ortogonal em W .Use a matriz obtida na parte b para encontrar a proje
Em cada parte, encontre det A T A e aplique o Teorema 6.4 . 3 para determinar se A tem vetores coluna linearmente independentes. A = - 1 3 2 2 1 3 0 1 1
Use a Fórmula (10) e o método do Exemplo 3 para encontrar matriz canônica da projeção ortogonal P : R 2 → R 2 No eixo x .[Observação: compare suas respostas com a Tabela 4 da Seção 4.9.]