Considere

é contínua em ? é derivável em ?

é contínua em ? é derivável em ?

Calcule e .

Determine os pontos críticos de .

Em quais intervalos é crescente?

Em quais intervalos é decrescente?

Determine, se houver, os pontos de mínimo local de .

Determine, se houver, os pontos de máximo local de .

Em quais intervalos, se houver, o gráfico de é côncavo para cima?

Em quais intervalos, se houver, o gráfico de é côncavo para baixo?

Determine, se houver, os pontos de inflexão do gráfico de .

Utilizando as informações obtidas nos itens anteriores, faça um esboço do gráfico de .

Já para ver se a função é derivável aplicamos o limite da definição da derivada e vemos se lateralmente os limites batem. A definição é essa aqui:

Vamos ver se os limites laterais desse termo batem, começando calculando :

Vamos fazer agora para :

Vamos usar L’Hospital para fugir da indeterminação:

Como vemos, os limites laterais da definição da derivada bateram, o que significa que é derivável em .

Para descobrir se a função é contínua no temos que calcular os limites laterais pelos dois lados e ver se eles são iguais. Como vemos, a função é uma em e outra em :

Ora, os limites laterais não batem, então a função não é contínua em.

Se a função é descontínua em ela necessariamente não é derivável!

Vamos calcular os dois limites pedidos:

O outro limite agora:

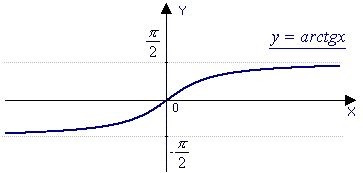
Caso não tenha entendido, esse aqui é o gráfico do arco tangente, cuja imagem fica sempre dentro do intervalo :

Pelos cálculos dos limites notamos que temos duas assíntotas verticais: . Como não temos descontinuidades da função nos três respectivos domínios nós não temos assíntotas verticais.

Vamos derivar a função :

Na região de temos que , que é negativo para todo .

Em a derivada é a , uma parábola com concavidade para baixo. Entre suas raízes, e , seu sinal é positivo. Já entre e será negativo.

Já no domínio de temos o termo para a derivada, que é negativo para todo valor de , já que exponenciais são sempre positivas e tem um sinal negativo ali.

Conclui-se, há dois pontos críticos, um em e outro em (vimos no Passo que a derivada nesse ponto, , vale ).

Para analisar o crescimento e decrescimento da função nós devemos observar o sinal da derivada. Como visto no Passo , a derivada será positiva para todo , para ou para , sendo nula só em e . A derivada é positiva para Ou seja, a função é sempre crescente, não havendo região de decrescimento, com o detalhe da derivada ser nula em :

Os pontos críticos são e . No primeiro, temos derivada negativa antes e positiva depois, no segundo temos derivada positiva antes e negativa depois desse ponto. Nós vemos que é ponto crítico de mínimo e ponto crítico de máximo:

Vamos calcular e analisar seu sinal para descobrir quais são suas regiões de crescimento e decrescimento:

Vemos que onde a concavidade depende só do numerador :

Como esse domínio só vale para , temos só o como ponto de inflexão, sendo a derivada segunda negativa antes desse ponto e positiva depois

Para , que tem ponto de inflexão em:

Sendo positiva antes de e negativa depois , com ponto de inflexão em .

Em o termo é sempre positivo, sendo que há uma mudança de concavidade de antes do (côncava para baixo) para depois desse ponto (côncava para cima).

Em resumo, temos:

Os únicos pontos em que a é nula ou muda de sinal são são em , e , então:

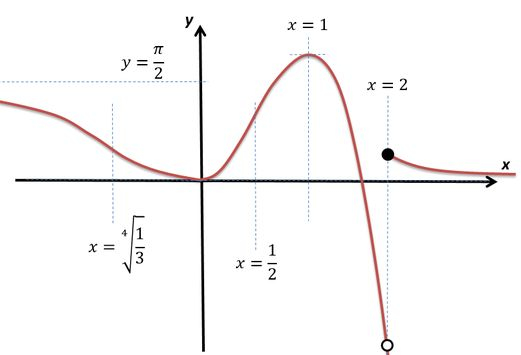
Vamos reunir todas as informações para fazer o nosso esboço:

Vamos fazer o esboço: