- Considere a dada por e suas derivadas e
f. Faça o esboço do gráfico de , identificando, caso existam, as assíntotas, os pontos de máximo e mínimo e os pontos de inflexão.
Passo 1
Oi, galerinha! Tudo bom? Aqui nós precisamos esboçar o nosso gráfico e para isso nós teríamos que busca algumas informações importantes sobre ele, como: as assíntotas, os pontos de máximo e mínimo e os pontos de inflexão.
Mas, então, galerinha, agora vou contar uma coisa boa: já obtivemos muitas dessas informações nos items de a, b, c, d e e dessa mesma questão. Sendo assim, vou colocar aqui embaixo um resuminho de algumas conclusões que podemos partir:
- A função é positiva em
- A função é negativa em
- Temos uma raiz em
- é uma função impar.
- A função cresce em .
- A função decresce em e
- A concavidade é para cima em e .
- A concavidade é para baixo em e .
- Temos uma assintota horizontal em .
- é um ponto de mínimo.
- é um ponto de máximo.
Agora vamos juntar todas essas informações em um gráfico!
Passo 2
Esboçando o gráfico ficamos com
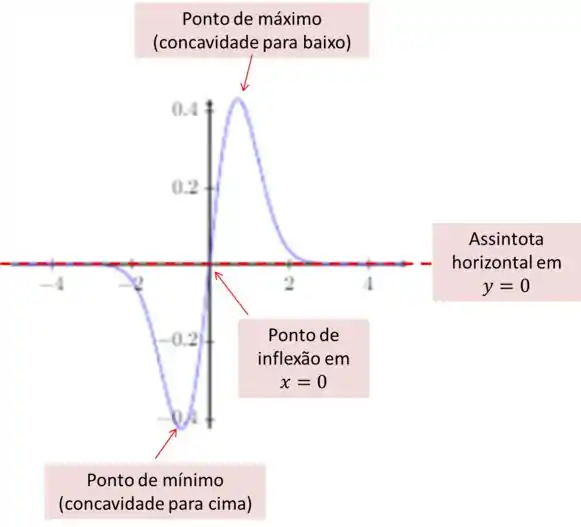
Resposta
Exercícios de Livros Relacionados
Faça um esboço cuidadoso de f e abaixo dele esboce o gráfico de f ’ como foi feito nos Exercícios 4 - 11 . Você pode sugerir uma fórmula para f ‘ ( x ) a partir de seu gráfico? f x = e x
Seja f x = x 2 .(a) Estime os valores de f ' ( 0 ) , f ' 1 2 , f ' ( 1 ) e f ' ( 2 ) fazendo uso de uma ferramenta gráfica para dar zoom no gráfico de f .(b) Use a simetria para deduzir os valores de
Faça um esboço cuidadoso de f e abaixo dele esboce o gráfico de f ’ como foi feito nos Exercícios 4 - 11 . Você pode sugerir uma fórmula para f ‘ ( x ) a partir de seu gráfico? f x = s e n x
Trace o gráfico da função f x = { x 2,- 1 ≤ x0 - x 2 ,0 ≤ x ≤ 1 f é contínua em x=0 ? f é derivável em x=0 ?
Esboce o gráfico de f à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de f . f x = x 2 ,- 3 ≤ x ≤ 2