Considere a função .
Determine:
os limites de quando tende a e quando tende a ;
os intervalos onde é crescente e aqueles onde é decrescente;
os pontos de máximo e mínimo locais e/ou globais (abscissas e ordenadas);
os intervalos onde a concavidade é para cima (função é convexa) e aqueles onde é para baixo (função é côncava);
os pontos de inflexão de .
Esboce o gráfico de , respeitando todos os aspectos do gráfico identificados no item .
Passo 1
Vamos termo a termo:
Para calcular os limites a gente tem que olhar para o grau desse polinômio . A gente sabe que o termo de maior grau é quem vai determinar para onde vai a função. Como temos ali no o como esse maior grau, vamos observar para onde ele iria em cada caso.
Para o explode para o mesmo valor, . Entretanto, como o expoente é ímpar, ele vai para quando . Assim, seguem os limites pedidos:
Passo 2
Quando a gente quer analisar o crescimento da função temos que analisar o sinal da derivada primeira do gráfico:
Partiu fazer o quadro de sinais para esse cara:
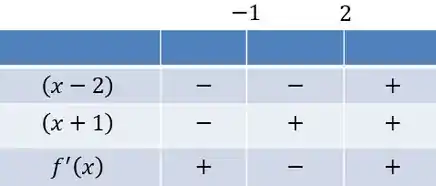
Conclusão: o decresce para e cresce no resto do domínio.
Passo 3
Os pontos onde temos máximos e mínimos, os pontos críticos, são aqueles onde e muda-se o regime de crescimento. Como a gente vê, isso acontece em e em . Para o primeiro ponto, a derivada é positiva antes e negativa depois, gerando um máximo local. Para o segundo valor, a derivada é negativa antes e positiva depois, um ponto de mínimo local.
Assim, máximo local ocorre em e o mínimo local em
Passo 4
Concavidade pede que trabalhemos com a derivada segunda:
Dá para ver que esse cara é positivo para valores maiores que e negativo para menores. Dá para visualizar então que a função é côncava para cima para valores de e para baixo no resto do domínio!
Passo 5
Ponto de inflexão é onde muda a concavidade de . Isso só acontece no ponto , onde !
Temos um ponto de inflexão em !
Passo 6
Agora é só esboçar esse cara, lembrando dos pontos relevantes (críticos e de inflexão) dos limites que calculamos e das regiões de crescimento e decrescimento, assim como as concavidades:
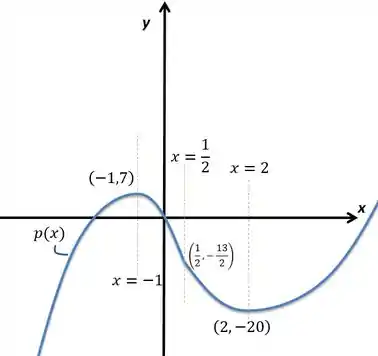
Resposta