Considere a função
a) Esboce o gráfico de , determinando:
- Os intervalos onde é crescente ou decrescente;
- Os seus máximos e mínimos locais;
- Os intervalos onde a concavidade é para cima ou para baixo.
b) Determine o número de raízes distintas de (isto é, para quantos valores distintos de tem-se . Justifique sua resposta.
Passo 1
A primeira coisa que nos é pedido é para determinar os intervalos onde a função é crescente ou decrescente, ou seja, vamos precisar da primeira derivada.
Colocando 12x em evidência temos:
Nossos pontos crítico (aqueles que podem zerar nossa função) serão então 0, -1 e 2.
Fazendo a análise dessa função temos então:
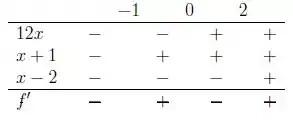
Percebemos então que entre e -1 a função é decrescente, depois crescente entre -1 e 0, decrescente novamente entre 0 e 2, e finalmente crescente de 2 a
Passo 2
Com essas informações podemos descobrir ainda quais são seus máximos e mínimos locais, que estarão em .
Isso nos trás que (-1,2) é um mínimo local, (0, 7) é um máximo local e (2,-25) é um mínimo local.
Passo 3
Para descobrirmos os pontos onde a concavidade é para cima ou para baixo, aplicamos a segunda derivada.
Tirando as raízes dessa equação do segundo grau para ver onde essa função zera.
Passo 4
Sabemos então que em aproximadamente a concavidade da função muda. Fazendo a análise do sinal da segunda derivada percebemos que entra e -0,55 a concavidade é positiva, entre -0,55 e 1,21 é voltada para baixo, e entre 1,21 e ela volta a ser voltada ara cima.
O esboço final fica então igual à:
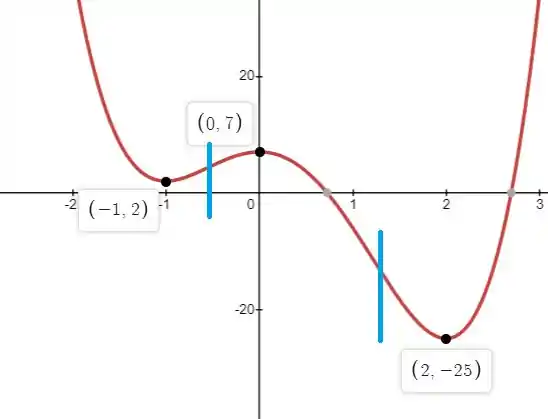
As barras azuis destacam os intervalos onde a função tem uma variação em sua concavidade.
Passo 5
b) Para determinar o número de raízes podemos simplesmente observar nosso esboço. Note que a função cruza apenas duas vezes o eixo x,logo, temos duas raízes.
Você deve observar ainda que antes de x=-1 e depois de x=2 a função está sempre tendendo a o que nos indica que ela nunca mais cruza o eixo x, mesmo quando x tende a .
Resposta
Ei, a resposta está no passo a passo :)