Considere a função cujo gráfico é dado na figura abaixo
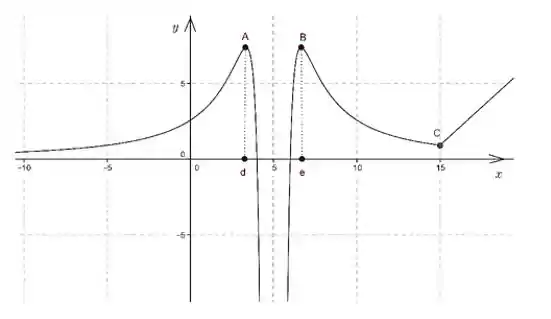
Com a ajuda da figura, responda às seguintes perguntas:
(i) Quais são as assíntotas horizontais e verticais ao gráfico da função ?
(ii) Identifique os intervalos onde a derivada da função é positiva e os intervalos onde a derivada da função é negativa
(iii) Quais são os pontos críticos de ? A função admite máximos ou mínimos locais nesses pontos?
(iv) A função é derivável em ? Caso seja, quanto vale ? A função é derivável em ? Caso seja, quanto vale ?
Passo 1
Assíntotas horizontais são as tendências da função quando ela converge enquanto explode para .
Nesse caso aí, repara que para a função cresce indefinidamente. Assim, não temos assíntota aí. Já para temos uma assíntota, pois o valor converge para quando decresce para esse valor.
Assíntotas verticais surgem quando a função explode para em descontinuidades do domínio.
No caso, só temos uma descontinuidade, e nela a função explode para . Logo, aparece uma assíntota vertical em .
Passo 2
Para determinar o sinal da derivada, basta olhar onde a função é crescente ou decrescente, sendo positiva e negativa, respectivamente.
Assim, é positiva em , e ; negativa em e .
Passo 3
Nos pontos críticos, procuramos onde a derivada é nula, ou a função tem um bico. Isso acontece em picos do gráfico, vales, e os próprios “bicos” da função.
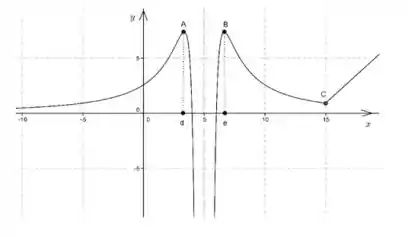
No caso, temos dois picos (máximos locais) nos pontos e (marcados com e ). Além disso, há um “bico” onde a função muda de sinal em , correspondendo a um mínimo local.
Passo 4
Em , vemos que a função assume um pico, um máximo local, com isso, vemos que ali não só é um ponto crítico, como a derivada é nula, ou seja:
Além disso, em a função tem um “bico”. Isso quer dizer que ela muda abruptamente a sua derivada, tendo as derivadas laterais diferentes, o que significa que ela não é derivável nesse ponto: