Considere a função

definida para .

1. Determine a(s) assíntota(s), calculando os imites necessários.
2. Encontre os intervalos de crescimento e decrescimento, bem como extremo(s) local(is).
3. Analise a concavidade e encontre os pontos de inflexão.
4. Esboce o gráfico

As assíntotas verticais só existem se a função tiver descontinuidade. Nesse caso, a função é descontínua para . Por isso, vamos verificar os limites para e .

Assim, é uma assíntota vertical.

O mesmo irá acontecer para :

Para saber os intervalos de crescimento e decrescimento temos que analisar o sinal da derivada de . Então vamos começar derivando a função:

Agora vamos descobrir seus pontos críticos:

Agora vamos analisar o sinal da derivada:

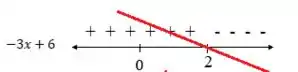
1º) Primeiro comecemos com o sinal da reta dada no denominador:

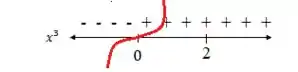
2º) Já o denominador, o , tem mais ou menos essa cara aqui oh:

A divisão dos sinais do cima pelo de baixo nos dará os sinais da primeira derivada, veja só:

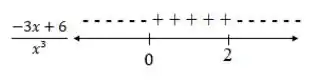
Esses sinais são cruciais para encontrar onde a função cresce ou decresce, pois como sabemos onde a derivada é negativa, a função decresce, já onde a derivada é positiva... Bem, acho que você já entendeu neh? Podemos resumir assim então:

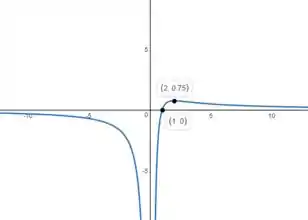
Veja bem que por essas setinhas que representam onde a função cresce e decresce, até podemos saber onde a função tem um ponto de máximo local: no , afinal a seta cresce antes do 2 e depois decresce.

Cuidado! Não podemos falar que é um ponto de mínimo local, pois zero nem pertence ao domínio da função. é um ponto problemático, lembra? Inclusive descobrimos que é assíntota vertical

Temos que descobrir onde a função é côncava pra cima ou côncava pra baixo. Como fazer isso? Analisando o sinal da segunda derivada. Então vamos derivar :

Perceba uma coisa interessante. Como o denominar possui expoente par, ele será sempre positivo. Logo, o sinal da segunda derivada só depende de .

Analisando o sinal e verificando a concavidade:

Quando

Quando

Agora é só colocar tudo que encontramos no plano cartesiano e esboçar o gráfico.