Considere a função .
- Determine as retas assíntotas verticais e horizontais (caso existam), calculando os limites necessários.
- Encontre os intervalos de crescimento e decrescimento, bem como os pontos críticos. Determine os pontos de máximo e mínimos locais, caso existam.
- Analise a concavidade e encontre os pontos de inflexão.
- Esboce o gráfico da função, destacando os pontos críticos e os pontos de inflexão, bem como as retas assíntotas.
Passo 1
É sempre bom começarmos as questões de gráfico determinando o domínio da função, mesmo que a questão não peça diretamente. Isto ajuda tanto na hora do esboço, quanto na identificação de assíntotas verticais, que é o que a questão nos pede na letra a), por exemplo.
Mas o que seria o domínio de uma função ? Basta você responder a seguinte pergunta: quais os possíveis valores que assume? A resposta desta pergunta é o domínio da função. Tenta sempre lembrar dos casos que as funções não existem.
Alguns exemplos de valores de que não pode acontecer são: divisões por zero; raízes de ordem par (, n é par) de números negativos e logaritmos de zero ou números negativos.
Então, começaremos verificando o domínio. Para isto, temos que nos perguntar. Será se existe algum valor de que a função não existe em si? Percebam que a função é dado pelos produtos de e .
A primeira é uma função polinomial, e a segunda uma função exponencial. Ambas as funções existem para qualquer valor de pertencente aos reais. Portanto, o domínio da nossa função são os reais.
Mas sim, o que isto vai nos ajudar na parte das assíntotas? A dica para checar se existe assíntotas verticais, é verificar se existe algum ponto que não pertence ao domínio da função (que nesse caso não existe). Caso isto ocorra, checaremos os limites laterais e verificaremos se o resultado é . Por exemplo,
Se algum deles fosse verdade, teríamos uma assíntota .
Como não temos nenhum ponto que não pertence ao domínio, não temos assíntota vertical.
Só relembrando, a ideia de uma assíntota vertical é uma reta paralela ao eixo . À medida que , seja pelo lado que for, o valor da nossa tende a mais ou menos infinito (digamos que ela cresce bastante). Por causa deste comportamento, tende a tangenciar essa assíntota. Esta é a ideia de uma assíntota vertical
Agora, nos resta checar as assíntotas horizontais. E para isto, vamos verificar os limites no infinito. Se eles derem um valor (não importa o número), teremos uma assíntota horizontal (fazemos isso tanto para quanto ).
Logo, checando os limites no infinito, temos:
Já para , temos:
E assim, chegamos a uma indeterminação. Para resolvermos, vamos utilizar a regra de L’Hospital. Para isto, precisamos transformar nossa função para obter uma indeterminação do tipo ou . Para conseguirmos isto, vamos passar o termo para o denominador. Logo,
Agora sim, podemos aplicar a regra de L’Hospital.
Relembrando, a regra de L’Hospital nos diz que:
Isto somente se a condição da indeterminação for satisfeita. Portanto, o nosso limite pode ser escrito por:
Substituindo o valor de , temos
Novamente, outra indeterminação do tipo . Repetindo a regra de L’Hospital, temos:
Substituindo o valor de , temos
Portanto, temos uma única assíntota horizontal dada por .
E como funciona uma assíntota horizontal? A ideia é semelhante à da assíntota vertical, só que agora a nossa reta é paralela ao eixo (horizontal). Por sinal, neste caso, a assíntota é o próprio eixo .
Bom, continuando, à medida que (caso desta questão, poderia ser para outra questão), a curva de tende a tangencia a reta . Em outras palavras, . Percebam que a função tende a 0, e não é 0 !!!!!!!
Passo 2
Agora, vamos analisar o intervalo de crescimento e decrescimento da nossa função, obter os pontos críticos da nossa função e analisar os pontos de máximo e mínimo locais.
Vamos começar pelos pontos críticos e intervalo de crescimento e decrescimento. Para ambos os casos, precisaremos obter a primeira derivada da função.
Mas antes de derivarmos, vamos nos relembrar a relação destes dois parâmetros que queremos determinar com a primeira derivada. Começando pelos pontos críticos, eles são todos os pontos tais que a primeira derivada é igual a 0 ou não existe.
Portanto, precisamos derivar a função e verificar se esta derivada não existe em algum valor ou igualar a 0 e encontrar os valores de que satisfazem (seria uma espécie da raiz da derivada).
Certo, isto é em relação ao ponto crítico. Mas os intervalos de crescimento e decrescimento. Como obteremos? Bom, já usamos né? Então... está faltando e . Pronto, essa é exatamente a ideia!
Se para um determinado intervalo, então a função é crescente nele. Se , então a função é decrescente.
Bom, agora podemos partir para a derivada da função em si. Neste caso, precisamos aplicar a regra do produto. Aplicamos esta regra para funções que são obtidas pelo produto de outras duas (neste caso, temos o produto de por ).
Então, a regra do produto nos diz que a deriva de é a derivada da primeira função pela segunda mais o produto da primeira função pela derivada da segunda .
Portanto, temos:
Percebem que o termo aparece multiplicando os dois termos? Então, vamos coloca-lo em evidência. Logo,
Mas não só era o termo que aparecia em ambos os termos. Também temos o termo . Então, colaremos ele em evidência também! Portanto,
Reorganizando a nossa função, temos:
Para encontrarmos os pontos críticos, vamos fazer . Isto só ocorrerá quando ou (fatorar a nossa função e escrever ela em termos de produto torna a análise muito mais fácil, fica a dica!)
Agora, vamos analisar o intervalo de crescimento e decrescimento. Para isto, fica mais fácil montarmos uma tabela e analisar o sinal separadamente de cada um dos termos que compõem a nossa . Depois, é só fazer o produto destes sinais.
Se fizermos isto, teremos a seguinte tabela:

Portanto, a função é crescente quando tem sinal positivo, o que acontece no intervalo e . E ela é decrescente no intervalo
Para finalizarmos, vamos determinar os pontos de máximo e mínimo locais. Para isto, vamos utilizar o teste da primeira derivada. Começando pelo ponto crítico . Como a derivada muda de sinal positivo para negativo , então temos um ponto de máximo local.
Já para o ponto crítico , temos o comportamento inverso. A derivada muda de sinal negativo para positivo. Portanto, temos um ponto de mínimo local.
Passo 3
Para analisarmos concavidade e ponto de inflexão, temos que fazer um procedimento semelhante ao realizado no Passo 2. Só que agora, faremos para a segunda derivada da função, . Obtendo esta derivada através da regra do produto:
Vamos buscar as raízes do polinômio para poder fatorá-lo. Portanto,
Portanto, fatorando o polinômio, vamos obter a seguinte função :
Agora, vamos analisar o intervalo em que a função é côncava para cima ou para baixo. Para isto, fica mais fácil montarmos uma tabela e analisar o sinal separadamente de cada um dos termos que compõem a nossa . Depois, é só fazer o produto destes sinais.
Se fizermos isto, teremos a seguinte tabela:

Portanto, a função é côncava para cima quando tem sinal positivo, o que acontece no intervalo e . E ela é côncava para baixo no intervalo
E em relação aos pontos de inflexão? A dica é analisar os valores em que a segunda derivada é nula, . Isto só ocorrerá quando ou (fatorar a nossa função e escrever ela em termos de produto torna a análise muito mais fácil, fica a dica!).
E depois? Precisamos analisar se o sinal de modifica ao passar por estes dois pontos. Em outras palavras, o ponto de inflexão é aquele no qual a concavidade da nossa curva muda.
Portanto, os pontos de inflexão são: e
Passo 4
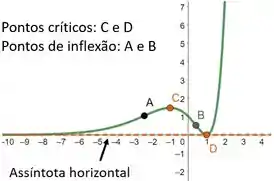
Para finalizar, vamos esboçar o gráfico da nossa utilizando o softwares para auxiliar. É importante ressaltar que os pontos de inflexão, os pontos críticos e as assíntotas devem ficar destacadas!
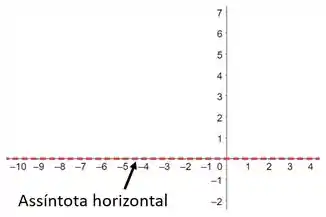
Então, vamos começar montando o gráfico devagar. Começamos desenhando a assíntota horizontal:
Percebam também que para qualquer valor de (isto ocorre pois é sempre positivo e também é sempre positivo). Então, a nossa função se aproxima da assíntota por cima . Logo, seria algo do tipo:
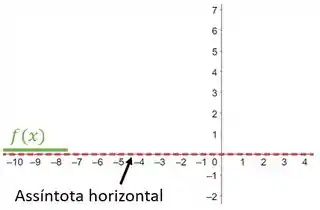
Uma coisa que ajuda na hora do esboço é calcularmos os valores de para os pontos críticos e pontos de inflexão (precisaremos destaca-los de qualquer forma). Então, relembrando, os pontos críticos são e os pontos de inflexão são .
Começando o cálculo pelos pontos críticos, se então:
Já para os pontos de inflexão, temos:
Não conseguir calcular estes valores não é problema. Lembrando que é um esboço, pelo comportamento (crescimento e decrescimento), vocês conseguem desenhar algo próximo do valor correto. Marcando estes pontos críticos, temos:
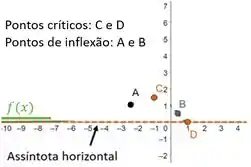
Para finalizarmos, é importante fazermos uma nova tabela compilando os dados dos passos 2 e 3 (crescimento/decrescimento e concavidade). Ao fazermos isto, fica muito mais fácil saber se a curva é côncava para cima e crescente num intervalo, ou se ela é côncava para baixo e decrescente, por exemplo. Portanto,
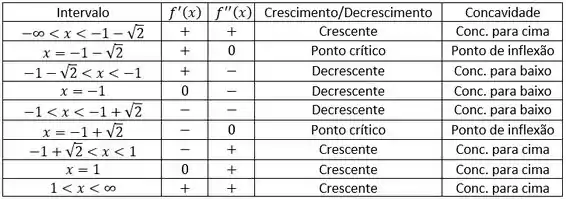
Pronto, com esta tabela acima e com aquele esboço inicial (fixados os pontos), agora é só os ligar e fazer o esboço do nosso gráfico. Sendo assim, temos o seguinte gráfico:
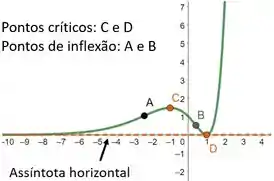
Resposta
- Não existem assíntotas verticais e a assíntota horizontal é ;
- A função é crescente no intervalo e e ela é decrescente no intervalo . Os pontos críticos são . O ponto é ponto de máximo local. Já o ponto é ponto de mínimo local.
- A função é côncava para cima no intervalo e . E ela é côncava para baixo no intervalo . Os pontos de inflexão são .
- O gráfico da função é: