Considere a função
(a) Esboce o gráfico da função .
(b) Considere um retângulo satisfazendo as seguintes condições:
- O vértice está no eixo negativo e possui abscissa
- O vértice está no eixo positivo e possui abscissa
- O vértice está no gráfico da função e possui abscissa
- O vértice está no gráfico da função e possui abscissa
(b.1) Escreva as ordenadas dos vértices e em termos de .
(b.2) Determine o domínio e a expressão da função , que fornece o perímetro do retângulo em termos de
Passo 1
Opa, calma aí! Esboço de gráfico? É galera, aqui a gente vai precisar usar um pouco a imaginação pra não precisar fazer aquele esboço demorado que envolve teste de derivadas e tudo mais. Pra começar, pensa na primeira lei de formação:
Se elevarmos os dois lados ao quadrado, temos:
Po, isso não te lembra nada não? É a equação de uma parábola! A diferença é que tem o e o trocado de lugar! Então pra gente esboçar basta a gente desenhar uma parábola, mas de lado. Saca só como fica:
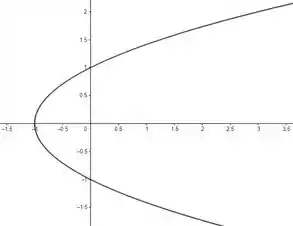
Mas vamos com calma! Pra começar, o sempre porque não existe raiz negativa. Então já reduzimos um pouco esse desenho:
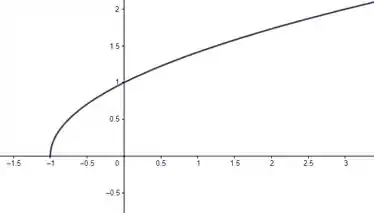
Agora ainda temos que pensar que a lei de formação só tá definida pra . Reduzimos ainda mais o desenho:
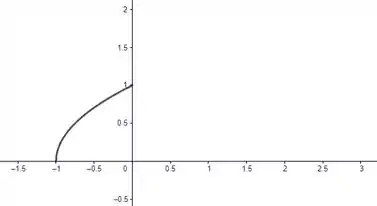
Agora, pra segunda parte da função,temos uma parábola de cabeça pra baixo, já que o número que multiplica o termo é negativo. Show de bola, nota ainda que em:
Se , . Sendo assim essa curva vai sair do eixo no mesmo ponto que a primeira curva parou! Pra fechar um esboço legal a gente pode escolher um qualquer perto do e ver se ele é maior que . Escolhendo :
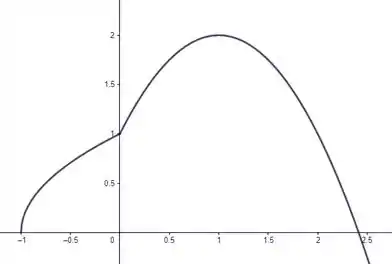
Beleza então pelo menos entre e a curva está subindo! Cara, isso quer dizer que o ponto de máximo de está em ! Beleza, nosso esboço no final das contas fica:
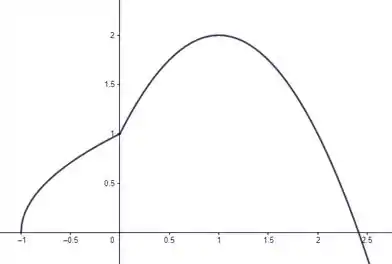
Passo 2
Tranquilo então, temos o nosso esboço da curva, vamos esboçar então pra entender melhor a questão o retângulo . Uma coisa de cada vez ok? Bora então marcar ponto a ponto:
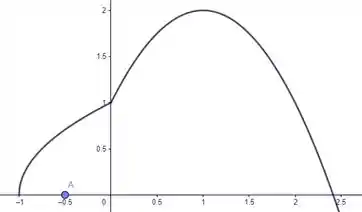
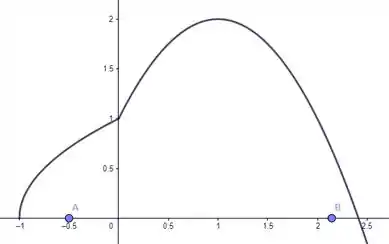
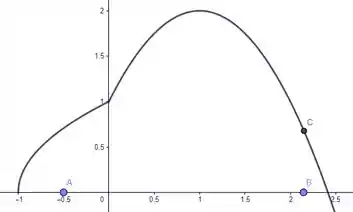
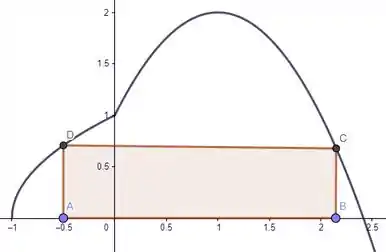
Pronto, agora fica mais tranquilo da gente entender. A questão quer as ordenadas dos pontos C e D. Veja pelo esboço que as duas estão “a mesma altura”, mas estão sobre leis de formação diferentes de . Esses pontos vão ser então:
Mas como a questão quer tudo em termos de e os pontos tão na mesma altura, responder a (b.1) é tranquilo, só escrever assim ó:
Passo 3
Pro cálculo do perímetro temos que pensar na base e na altura primeiro, e tudo em função de . A altura já ta dada pois é somente a altura dos pontos . Vamos ter:
Agora a base é um tico mais complicado. Veja só, podemos entender ela como:
Mas aí não temos uma função de Pra gente conseguir fazer temos que escrever como uma função de , isto é, , tranquilo? Pra isso, olha a sagacidade: se os pontos tem a mesma altura...
...então eles tem a mesma coordenada ! Igualando:
Perfeito! Fechamos a expressão da base:
E como o perímetro é nada mais nada menos que o dobro da soma da base com a altura, chegamos a expressão dele:
E pra fechar com chave de ouro, só responder o domínio! Pra isso, note que é um polinômio! Polinômios não são funções que “dão problema” então qualquer que eu dê pra função ele me retorna um , sem restrição! O domínio será:
Resposta