Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Esboço de Gráfico

Ver Teoria
Exercício 253123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

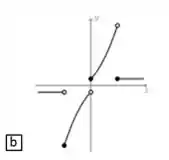
9. Considere as funções f , g definidas por

f x = x 2 ,   s e   x < - 1 x ,   s e - 1 ≤ x < 1 - x 2 ,   s e   x ≥ 1

E

g x = - x 2 - 1 4 ,   s e   x < 0 x 2 + 1 4 ,   s e   x ≥ 0

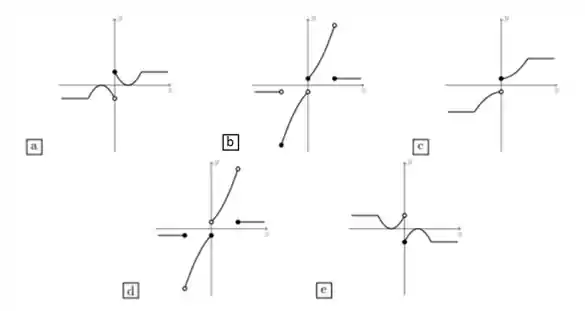
A figura que melhor representa o gráfico de f + g é:

Passo 1

Oi, galerinha! Tudo bom? O enunciado nos forneceu quem é f e g e pediu para indicarmos como seria o gráfico de f + g .

Mas repara que f e g são funções que mudam de comportamento de acordo com o intervalo.

f x = x 2 ,   s e   x < - 1 x ,   s e - 1 ≤ x < 1 - x 2 ,   s e   x ≥ 1

E

g x = - x 2 - 1 4 ,   s e   x < 0 x 2 + 1 4 ,   s e   x ≥ 0

Então vamos ter que construir uma nossa função e entender o comportamento dela para cada intervalo.

Bora lá!

Passo 2

Vamos começar para valores menores que x < - 1 .

Olhando para f x temos o seguinte comportamento,

f x = x 2

Olhando para g x vamos ter,

- x 2 - 1 4

Fazendo f + g ,

f + g = x 2 - x 2 - 1 4 = 1 4

Ou seja,

f + g = 1 4 ,   s e   x < - 1

Passo 3

Agora vamos pegar valores no intervalo - 1 < x < 0 .

Olhando para f x temos o seguinte comportamento,

f x = x

Olhando para g x vamos ter,

- x 2 - 1 4

Fazendo f + g ,

f + g = x - x 2 - 1 4 = - x 2 + x - 1 4

Ou seja,

f + g = - x 2 + x - 1 4 ,   s e - 1 ≤ x < 0

Passo 4

Agora vamos pegar valores no intervalo 0 < x < 1 .

Olhando para f x temos o seguinte comportamento,

f x = x

Olhando para g x vamos ter,

+ x 2 + 1 4

Fazendo f + g ,

f + g = x + x 2 + 1 4 = + x 2 + x + 1 4

Ou seja,

f + g = + x 2 + x + 1 4 ,   s e   0 ≤ x < 1

Passo 5

Agora vamos pegar valores no intervalo x ≥ 1 .

Olhando para f x temos o seguinte comportamento,

f x = - x 2

Olhando para g x vamos ter,

+ x 2 + 1 4

Fazendo f + g ,

f + g = - x 2 + x 2 + 1 4 = + 1 4

Ou seja,

f + g = + 1 4 ,   s e   1 ≤ x

Passo 6

Juntando tudo ficamos com

f + g = 1 4 ,   s e   x < - 1 - x 2 + x - 1 4 ,   s e - 1 ≤ x < 0 + x 2 + x + 1 4 ,   s e   0 ≤ x < 1 + 1 4 ,   s e   1 ≤ x

Ou seja, nosso gráfico tem que ser: uma constante para valores menores que - 1 (com uma bolinha aberta nesse ponto); uma parábola para baixo entre - 1 (com bolinha fechada) e 0 (com bolinha aberta); uma parábola para cima entre 0 (com bolinha fechada) e 1 (com bolinha aberta); e uma constante a partie de x = 1 (com bolinha fechada).

Logo a melhor opção que descreve essas características será:

Resposta

b

Exercícios de Livros Relacionados

Faça um esboço cuidadoso de f e abaixo dele esboce o gráfico de f ’ como foi feito nos Exercícios 4 - 11 . Você pode sugerir uma fórmula para f ‘ ( x ) a partir de seu gráfico? f x = e x
Seja f x = x 2 .(a) Estime os valores de f ' ( 0 ) , f ' 1 2 , f ' ( 1 ) e f ' ( 2 ) fazendo uso de uma ferramenta gráfica para dar zoom no gráfico de f .(b) Use a simetria para deduzir os valores de
Faça um esboço cuidadoso de f e abaixo dele esboce o gráfico de f ’ como foi feito nos Exercícios 4 - 11 . Você pode sugerir uma fórmula para f ‘ ( x ) a partir de seu gráfico? f x = s e n x
Trace o gráfico da função f x = { x 2,- 1 ≤ x0 - x 2 ,0 ≤ x ≤ 1 f é contínua em x=0 ? f é derivável em x=0 ?
Esboce o gráfico de f à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de f . f x = x 2 ,- 3 ≤ x ≤ 2