Considere
- Verifique que
- Ache as assíntotas horizontais e verticais caso existam.
- Identifique os intervalos onde a função é crescente e onde é decrescente.
- Encontre os valores máximo e mínimo locais e/ou globais caso existam.
- Identifique os intervalos de concavidade para cima e para baixo e os pontos de inflexão
- Usando as informações anteriores faça um esboço do gráfico de
e que
Passo 1
a)
Vamos começar encontrando a derivada de
Usando as regras de derivação
Que é igual ao valor dado no enunciado.
Passo 2
Vamos agora encontrar
Que é igual ao valor dado no enunciado.
Passo 3
b)
As assíntotas horizontais são moleza, basta achar
Passo 4
Começando pelo limite no infinito positivo
Como
Temos uma indeterminação do tipo , e podemos aplicar a regra de L’Hôpital
Vai continuar dando indeterminação , aplica regra de L’Hôpital de novo
Vai continuar dando indeterminação , aplica regra de L’Hôpital de novo
Ou seja, a reta é uma assíntota horizontal
Passo 5
Vamos para o limite no infinito negativo agora
Então
Ele vai para menos infinito porque o limite do exponencial vai para zero pela direita, ele sempre é maior que zero.
Não tem assíntotas verticais, pois não existe nenhum número real “” tal que:
Lembrai-vos: as verticais normalmente aparecem quando na função você consegue algum que dá uma divisão por zero.
Passo 6
c)
Para olharmos onde a função é crescente e decrescente, basta olharmos os sinais da primeira derivada.
Vamos montar o quadro de sinais desse produto
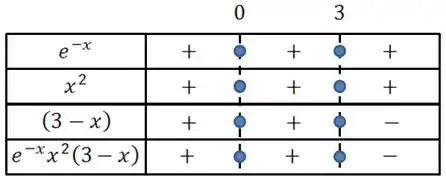
Lembrando que devemos achar onde cada parcela do produto é zero, e depois olhar os sinais antes e depois desses pontos!!
Repare que e são sempre positivos, eles na verdade não influenciam no sinal da derivada.
Os intervalos onde a função é crescente são aqueles onde a derivada é positiva:
E decrescente onde ela é negativa:
Temos
Passo 7
d)
Com o quadro de sinais montado lembra que quando a função vai de decrescente para crescente esse ponto é de mínimo local, e quando a função vai de crescente para decrescente ela é um ponto de máximo local.
Como vimos no item b),
Como a função não tem assíntotas verticais, e não existe momento que ela se aproxima de infinito positivo esse ponto é na verdade máximo global,
Passo 8
e)
Para analisarmos a concavidade devemos olhar os sinais da segunda derivada
Vamos montar o quadro de sinais desse produto
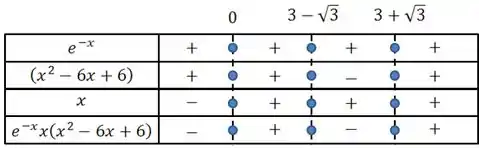
Lembrando que devemos achar onde cada parcela do produto é zero, e depois olhar os sinais antes e depois desses pontos!!
Temos
O ponto de inflexão acontece quando a concavidade muda, temos três pontos de inflexão
Passo 9
f)
Vamos desenhar o gráfico,
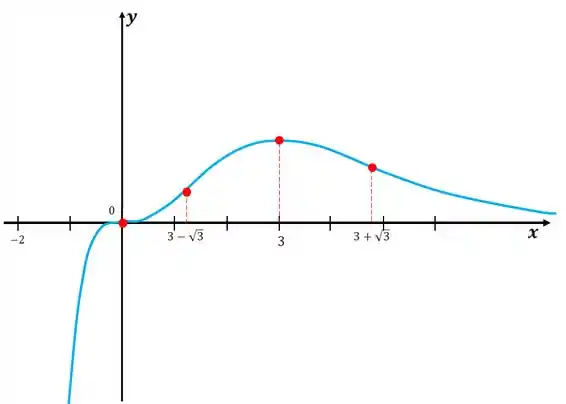
Resposta
Ei, a resposta está no passo a passo :)