Esboço de Curvas
Dada a função , determine:
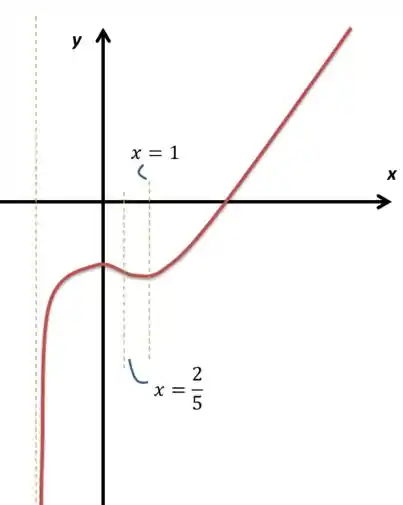
o esboço do gráfico de ;
Passo 1
Vamos juntar as informações até aqui:
-
-
-
-
-
Podemos adicionar a essas informações o valor de quando nos guiar no gráfico sobre onde cortamos o eixo e onde está a raiz do gráfico.
Ou seja, temos apenas uma raiz positiva já que o gráfico apenas cresce antes de e depois de , sendo unicamente decrescente entre eles, que são dois valores negativos. Vamos esboçar então:
Resposta
Exercícios de Livros Relacionados
Faça um esboço cuidadoso de f e abaixo dele esboce o gráfico de f ’ como foi feito nos Exercícios 4 - 11 . Você pode sugerir uma fórmula para f ‘ ( x ) a partir de seu gráfico? f x = e x
Seja f x = x 2 .(a) Estime os valores de f ' ( 0 ) , f ' 1 2 , f ' ( 1 ) e f ' ( 2 ) fazendo uso de uma ferramenta gráfica para dar zoom no gráfico de f .(b) Use a simetria para deduzir os valores de
Faça um esboço cuidadoso de f e abaixo dele esboce o gráfico de f ’ como foi feito nos Exercícios 4 - 11 . Você pode sugerir uma fórmula para f ‘ ( x ) a partir de seu gráfico? f x = s e n x
Trace o gráfico da função f x = { x 2,- 1 ≤ x0 - x 2 ,0 ≤ x ≤ 1 f é contínua em x=0 ? f é derivável em x=0 ?
Esboce o gráfico de f à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de f . f x = x 2 ,- 3 ≤ x ≤ 2